数列概念：数列的通项公式及解答题技巧

考点剖析：了解数列的定义、数列与函数的关系，理解数列的通项公式，会通过观察找规律归纳猜想数列的通项公式，会根据数列的通项公式求某项的值.

1.数列的定义

（1）数列：按一定次序排列的一列数称为数列.一般用a1，a2，a3，…，an表示，记作{an}.

（2）数列的项：数列中的每一个数都称为这个数列的一项，第一项又称为首项.

2.数列的分类：只有有限项的数列称为有穷数列，有无穷多项的数列称为无穷数列.

3.数列的通项公式：一个数列{an}中的第n项an与项数n之间的关系，如果可以用一个公式an=f（n）来表示，这个公式就称为这个数列的通项公式.

（本章所用的项数n，m∈N*，之后不再特别说明）

【题型1】根据数列前n项值，求数列的通项公式

例　根据数列的前几项，写出下列各数列的一个通项公式.

（1）1，4，9，16，…

（2）

（3）

（4）

解：（1）把数列中的各项与它们的项数列表进行比较.

项数n：1，　2，　3，　4，　…，n，…

项an：1=12，4=22，9=32，16=42，…，n2，…

所以数列的通项公式为：an=n2.

（2）把数列中的各项与它们的项数列表进行比较.

项数n：1，2，　3，　4，…，　n，　…

项an：

所以数列的通项公式为：

（3）把数列中的各项与它们的项数列表进行比较.

项数n：　1，　2，　3，　4，　…，　n，　…

项an：

所以数列的通项公式为：

（4）把数列中的各项与项数列表进行比较.

项数n：1，2，　3，4，　5，…，　n，　…

项an：

所以数列的通项公式为：

赢在起点

根据数列的前几项，写出下列各数列的一个通项公式.

（1）1，3，5，7，9，…　an=____________；

（2）2，4，6，8，10，…　an=____________；

（3），…　an=____________；

（4），…　an=____________.

【题型2】根据数列通项公式，求数列中某些项的值(www.xing528.com)

例　已知下列数列的通项公式，分别求出它们前4项.

（1）an=2n+1，　（2）an=

解：（1）a1=2×1+1=3　a2=2×2+1=5

a3=2×3+1=7　a4=2×4+1=9

（2）a1=　a2=

a3=　a4=

赢在起点

根据数列的通项公式，求出它们前4项的值.

（1）an=-2n+3，　（2）an=2n-1.

【题型3】根据数列递推公式，求数列中某些项的值

例　已知数列{an}的第1项是2，以后各项由公式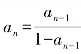给出，写出这个数列的前4项.

解：a1=2　a2=

赢在起点

已知数列{an}满足递推公式an=2an-1+1（n≥2），其中a4=15，写出这个数列的前3项 .

一、填空题

1.写出下列各数列的通项公式.

（1）1，3，5，7，…则an=____________；

（2）2，4，6，8，…则an=____________；

（3）1，4，9，16，…则an=____________；

（4）-1，3，-5，7，…则an=____________；

（5）3，7，11，15，…则an=____________；

（6），…则an=____________.

2.数列{an}中，已知，那么a5=____________.

3.已知数列an=n（n+1），则56是这个数列第________项.

二、选择题

1.数列{an}中，已知，则a5=（　）.

2.数列{an}中，已知前4项是，…则第5项是（　）.

3.已知数列{an}的前4项分别为1，0，1，0，…则下列等式中不能作为它的通项公式的是（　）.

4.数列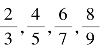，…的第10项是（　）.

5.数列{an}中，已知an+1=2an+3，a1=2，则a5=（　）.

A.17　B.36　C.77　D.78

三、解答题

根据数列的前几项，写出下列数列的一个通项公式.

（1）0，3，8，15，24，…　（2）