解三角形问题正弦、余弦定理及面积公式详解

考点剖析：理解熟记正弦定理、余弦定理及三角形面积公式，并会用这三组公式灵活解答简单的与三角形相关的实际问题.

三角形的相关公式

（1）直角三角形

勾股定理：c2=a2+b2.

边角关系：

（2）任意三角形

正弦定理：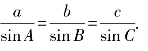

余弦定理　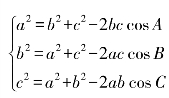可变形为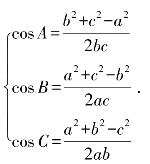

面积公式：①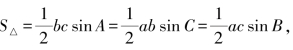

②

大多数情况下，已知和求的元素涉及两边和两个角时，通常用正弦定理公式，涉及三边和一个角时，通常用余弦定理公式，两边夹一角求面积用面积公式①.

【题型1】判断三角形的形状

例　在△ABC中，已知a=12，b=15，c=10，试判定△ABC的形状.

解：因为b2=a2+c2-2ac cos B

所以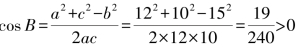

所以B角为锐角，所以△ABC为锐角三角形.

【锦囊妙计】据三角形“大边对大角，小边对小角”定理，只要求出最大角是锐（直、钝）角，则三角形为锐（直、钝）角三角形.即最大角的余弦值：①为正时，三角形为锐角三角形；②为0时，三角形为直角三角形；③为负时，三角形为钝角三角形.

赢在起点

1.在△ABC中，已知a=10，b=8，c=5，则△ABC是____________三角形.

2.在△ABC中，已知a=15，b=17，c=8，则△ABC是__________三角形.

【题型2】正弦定理、余弦定理、三角形面积公式的简单应用

例1　在△ABC中，已知a=3，c=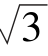，∠A=120°，求∠C及面积.

解：因为，所以

因为0＜C＜180°，所以∠C=30°或∠C=150°，

但当∠C=150°时，∠A+∠C=270°＞180°不合题意，应舍去，

所以∠C=30°，

所以∠B=180°-（∠A+∠C）=180°-150°=30°，

所以

例2　如右图所示，在四边形ABCD中，已知AB=3，BC=4，DC=4，∠ABC=120°，∠ADC=60°，求AD的长为多少？

解：连接AC，在△ABC中，AC2=AB2+BC2-2AB·BC cos∠ABC

AC2=32+42-2×3×4 cos 120°=37，

在△ADC中，AC2=AD2+DC2-2AD·DC cos∠ADC

37=AD2+42-2×AD×4 cos 60°

AD=7　或　AD=-3（舍去）

所以AD=7.

例3　在△ABC中，已知a=6，b=4，∠C为锐角，且cos C是方程4x2-1=0的一个根，求该三角形的周长和面积.

解：因为4x2-1=0，所以，又因为∠C为锐角，所以

因为c2=a2+b2-2ab cos C，

所以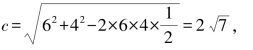

所以△ABC的周长为：10+2.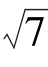

因为，∠C为锐角，所以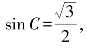

所以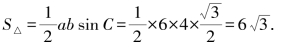

赢在起点

1.在△ABC中，已知a=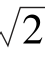，c=2，∠A=30°，则∠C=________，S△ABC=________.

2.在△ABC中，已知a=3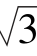，b=2，∠C=150°，则c=__________.

【题型3】正弦定理、余弦定理、三角形面积公式的实际应用

例　为了测量不能达到底部的一古塔的高，可以在地面上引一条基线MN，它和塔底在同一水平面上，且延长后不过塔底，如右图所示，现测量得=80 m，∠FMN=60°，∠FNM=75°，仰角∠ENF=30°，求塔高

解：在△MNF中，∠FMN=60°，∠FNM=75°，则∠MFN=45°，由正弦定理得：

答：塔高为40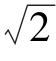m.

赢在起点

如右图所示，海上有A、B、C 3个小岛，其中A、B两个小岛相距10海里，从A岛望B岛和C岛成45°的视角，从B岛望A岛和C岛成75°的视角，则B岛和C岛间的距离为__________海里.

一、填空题

1.在Rt△ABC中，a=3，b=1，∠C=90°，则c=_______，∠A=_______，∠B=_______.

2.已知△ABC中，a=6，b=3，∠C=120°，则c=________，S△=________.

3.已知△ABC中，∠B=45°，c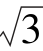=2，b=2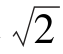，则∠C=________.

4.已知三角形三边之比为3∶4∶5，则该三角形的形状是________.

5.已知△ABC中，a=3，b=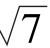，c=2，则∠B=__________.

6.在△ABC中，已知a=3，b=4，∠C=60°，则S△ABC=__________.

二、选择题(www.xing528.com)

1.如果△ABC三内角A、B、C成等差数列，则∠B=（　）.

A.90°　B.60°　C.30°　D.45°

2.△ABC中，已知a=3，b=5，c=7，则∠C的度数是（　）.

A.30°　B.60°　C.120°　D.150°

3.已知△ABC中，c=2，b=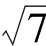，a=3，则∠B=（　）.

4.已知△ABC中，a=6，b=5，c=8，则△ABC为（　）.

A.锐角三角形　B.钝角三角形　C.直角三角形　D.以上都可能

5.已知△ABC中，a=2，b=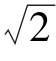，c=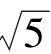，则△ABC为（　）.

A.锐角三角形　B.钝角三角形　C.直角三角形　D.以上都可能

一、填空题

1.在△ABC中，a=4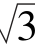，b=2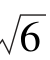，∠B=30°，则∠A=________.

2.在△ABC中，∠B=45°，∠C=75°，a=6，则∠A=________，b=________，c=________，S△=________.

3.在△ABC中，b=8，c=6，∠A=60°，则a=________.

4.在△ABC中，a=6，c=3，∠C=120°，则b=________，S△=________.

5.在△ABC中，∠A=30°，∠B=120°，b=12，则a=________，S△=__________.

6.如图所示，要测量一水塘两侧A、B两点间的距离，选择适当位置C，用仪器测得∠ACB为锐角，且sin∠ACB=0.6，AC=20米，BC=40米，则A，B两点间的距离为________米（结果保留整数，已知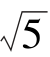≈2.236）.

二、选择题

1.在△ABC中，a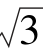=3，b=3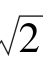，∠A=60°，则∠B=（　）.

A.30°　B.45°　C.135°　D.45°或135°

2.在△ABC中，∠B=45°是的（　）.

A.充分条件　B.必要条件

C.充要条件　D.既不充分又不必要条件

3.三角形的三条边的长度分别为4，3，，则它的最大的内角的大小是（　）.

A.45°　B.60°　C.120°　D.135°

4.边长为5，7，8的三角形的最大角与最小角之和为（　）.

A.90°　B.120°　C.135°　D.150°

5.在△ABC中，若a2+b2-c2＜0，则△ABC为（　）.

A.锐角三角形　B.钝角三角形　C.直角三角形　D.形状不能确定

三、解答题

1.如右图所示，在梯形ABCD中，已知AB=8，BC=5，对角线AC=7，BD平分底角∠ABC，求：（1）∠ABC的度数；（2）梯形ABCD的面积.

2.△ABC中，设3个内角A、B、C所对的边依次为a、b、c，已知A=60°，b+c=10，△ABC的面积为，求a的值.

3.如右图所示，A是一座灯塔，B为一个港口，一艘轮船由B港出发，航行40海里达到C，现测得B港在C的南偏东40°的方位上，灯塔A在C的北偏东20°的方位上，已知B港和灯塔A之间的距离为海里，求C到灯塔A的距离d.

4.△ABC中，设3个内角A，B，C所对的边依次为a，b，c，已知a=，b=3，A为锐角，且cos A是方程6x2-x-2=0的根，求△ABC的面积.

1.小华到农村体验生活，他站在距一座山的水平中心O点200米的地方D处看到山顶上有一根电线杆AB，如右图所示，他用测绘仪在D点测得仰角∠ODB=45°，∠ODA=60°，你能帮他算出这根电线杆有多长吗？

2.如右图所示，有一个人站在河的AB边上，测得=100米，AB∥CD，他用测量工具测得∠DAB=30°，∠DBA=105°，∠BAC=120°，你能计算出CD之间的距离吗？

自我评价

（满分100分，时间45分钟）　评价结果：__________

一、填空题（每题5分，共50分）

1.函数的最大值是________________.

2.函数的最小正周期是________________.

3.函数y=sin x+cos x的最大值是________________.

4.函数y=cos2（3x）-sin2（3x）的最大值是____________，最小正周期是____________.

5.函数y=-2 sin 2x+3的最大值是________________.

6.在Rt△ABC中，∠C=90°，a=4，b=2，则c=________________.

7.在Rt△ABC中，∠C=90°，a=4，tan A=2，则b=________________.

8.在△ABC中，a=3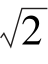，A=45°，B=60°，则b=________________.

9.在△ABC中，a=4，b=6，∠C=30°，则S△ABC=________________.

10.在△ABC中，a=3，∠B=120°，c=4，则b=________________.

二、选择题（每题5分，共20分）

1.在Rt△ABC中，∠C=90°，a=5，b=12，则cos A=（　）.

2.△ABC的三边a=7，b=8，c=11，则△ABC是（　）三角形.

A.直角　B.锐角　C.钝角　D.无法判定

3.已知sin α=，α∈（0，2π），则α=（　）.

4.已知，α∈（0，π），则α=（　）.

三、解答题（每题10分，共30分）

1.如右图所示，小李到南岸滨江路AB散步，他从B点看到河对岸的朝天门大酒店建筑物C，这时∠ABC=30°，他继续往前走了3000米到达E处，这时∠AEC=45°，试求朝天门大酒店建筑物C与南岸滨江路AB的距离CD？（保留一位小数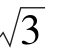）（≈1.73）

2.在△ABC中，已知b=7，c=3，A为锐角，且cos A是方程3x2+2x-1=0的一个根，求该三角形的周长和面积.

3.某建筑公司在高出地面20米的小山顶上建造了一座电视塔CD，如右图所示.设B为电视塔的正下方水平面上的点，在坡脚取一点A，测得∠CAD=45°，∠CAB=α且，则该电视塔的高度是多少米？