三角函数图像与性质及考试指南

考点剖析：了解正弦函数、余弦函数、正弦型函数的概念和图像；理解正、余弦函数的性质；掌握用正弦余弦函数的性质和图像，能解决简单的三角函数问题，会求正弦型函数y=A sin（ωx+φ）的最值和周期，根据已知正余弦函数值求指定区间［0，2π）上的特殊角.

1.三角函数的图像及性质如下表所示：

2.会求正（余）弦型函数的周期和最值.

（1）正弦型函数y=A sin（ωx+φ）、余弦型函数y=A cos（ωx+φ）中，，最小正周期

（2）形如函数y=a sin（ωx+φ）+b cos（ωx+φ），它的最值和周期如下：

ymax=，最小正周期

（3）形如函数y=A tan（ωx+φ）的最小正周期

（4）若函数不是以上类型，求它的最值和周期则把函数化成正（余）弦型即可.

3.利用函数的单调性比较函数值的大小.

4.根据已知三角函数值求指定区间［0，2π）上的角.

【题型1】比较大小

例　（1）sin 50°________sin 68°；（2）sin____________________

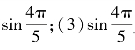（4）sin 181°________sin 542°；（5）sin__________

解：（1）＜；（2）＞；（3）＞；（4）＞；（5）＞.

赢在起点

比较大小

（1）sin 20°________sin 40°；（2）cos 130°________cos 160°；

（3）sin __________sin ；（4）cos 280°________cos 290°.

【题型2】求三角函数的最小正周期和最值

例　求下列三角函数的最小正周期和最值.

（1）y=-sin 2x+1，（2）y=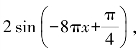

（3）y=（4）y=cos 4x-sin 4x，

（5）y=，（6）y=sin x+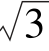cos x.

解：（1）T=π，ymax=1+1=2，ymin=-1+1=0.

（2）T=，ymax=2，ymin=-2.

（3）T=3π，无最值.

（4）y=cos 2x，T=π，ymax=1，ymin=-1.

（5）y=sin x，T=2π，ymax=，ymin=

（6）因为所以

y=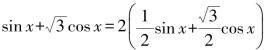

=

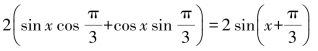
T=2π，ymax=2，ymin=-2.

赢在起点

1.函数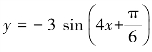的最小正周期是________，最大值为________，最小值为________.

2.函数y=sin x cos x=__________，它的最小正周期是________，最大值为________，最小值为________.

3.函数y=sin x+cos x=__________，它的最小正周期是________，最大值为________，最小值为__________.

【题型3】根据正余弦函数值求指定区间［0，2π）上的角

例　（1）已知，若x∈［0，2π），求x的值.

（2）已知，若x∈［0，2π），求x的值.

解：（1）因为则

因为sin x＞0，所以x为第一或第二象限的角，

所以或x2=π-x0=

（2）因为则

又因为cos x＜0，所以x为第二或第三象限的角，

所以x1=π-x0=或x2=π+x0=

【锦囊妙计】已知函数值求角的解题步骤：

（1）求出函数值的绝对值对应的锐角x0；

（2）根据函数值的符号，判断所求角所在的象限；

（3）求出［0，2π）内满足条件的角x，如右图所示.

【题型4】三角函数图像性质的简单应用

例1　（1）将函数f（x）=的图像向左平移φ（0≤φ≤2π）个单位后得到f（x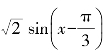）=的图像，则φ=（　）.

（2）以下函数①y=3x+1，②y=（x≠0），③y=sin x，④y=cos x在其定义域为奇函数的有（　）.

A.①②　B.②③　C.③④　D.②④

（3）函数f（x）=的单调递增区间为（　）.

A.［5π，9π］　B.［-5π，-π］　C.［6π，10π］　D.［4π，7π］

（4）函数f（x）=（sin x-cos x）2+1的奇偶性是（　）.

A.奇函数　B.偶函数　C.既奇又偶函数　D.非奇非偶函数

（5）已知ω＞0，0＜φ＜π，直线和是f（x）=sin（ωx+φ）的两条相邻对称轴，则φ=（　）.

解：（1）A；（2）B；（3）A；（4）D；（5）　B.

例2　已知函数f（x）=，（1）求f（x）的最小正周期；（2）若，求的值.

解：（1）由条件知，故f（x）的最小正周期为π.

（2）因为，所以

例3　已知函数f（x）=2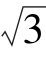sin x cos x+2 cos2x，（1）求f（x）的最小正周期；（2）若x∈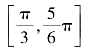，求f（x）的最小值和最大值.

解：（1）f（x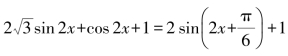）=，所以最小正周期T=π.

（2）因为，所以

所以fmax（x）=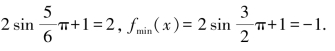

赢在起点

1.将函数f（x）=sin 2x的图像向左平移φ（0≤φ≤2π）个单位后得到f（x）=sin的图像，则φ=__________.

2.将函数f（x）=sin x的图像向右平移φ（0≤φ≤2π）个单位后得到f（x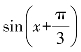）=的图像，则φ=__________.(www.xing528.com)

3.函数y=tan 2x的奇偶性是________，函数y=cos x+2的奇偶性是__________.

4.将函数f（x）=2 sin2x+2 3sin x cos x-1化为正弦型函数为__________.

5.函数f（x）=，则它的最小正周期是________，若则

一、填空题

1.已知函数：①y=2x+3，②y=x2+2x+1，③y=sin x cos x，④y=，则其中奇函数有________个.

2.函数y=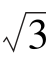sin x-cos x的最大值为________.

3.函数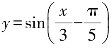的最小正周期是________，最大值为________，最小值为________.

4.函数的最小正周期是________，最大值为________，最小值为________.

5.函数y=3 sin x+2的最小正周期是________，最大值为________，最小值为________.

6.函数y=-4 sin 2x+1的最小正周期是________，最大值为________，最小值为________.

7.函数的最小正周期是________，最大值为________，最小值为________.

8.函数y=sin x的奇偶性是________，函数y=cos x的奇偶性是________.

9.函数y=sin x cos x的奇偶性是________，函数y=cos2x-sin2x的奇偶性是________.

10.比较大小：sin 18°________sin 43°，cos 18°________cos 38°，cos（-15°）________cos 35°，sin 18°________cos 38°，sin 98°________sin 138°，cos 208°________cos 238°，sin（-35°）________sin（-13°）.

二、选择题

1.“sin α=”是“α=”的（　）.

A.充分而不必要条件　B.必要而不充分条件

C.充要条件　D.既不充分也不必要条件

2.tan α=tan β是α=β的（　）.

A.充分而不必要条件　B.必要而不充分条件

C.充要条件　D.既不充分也不必要条件

3.函数f（x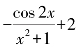）=是（　）.

A.奇函数　B.偶函数

C.既奇又偶函数　D.非奇非偶函数

4.y=3 sin x+4 cos x的最小值是（　）.

A.7　B.-7　C.5　D.-5

5.如果，则一定成立的是（　）.

A.cos α＜cos β　B.sin α＜sin β　C.cos α＞sin β　D.cos α＜sin β

6.已知函数f（x）=A sin ωx的图像如下，则f（x）的（　）.

A.T=1，ymax=1　B.T=2，ymax=1

C.T=1，ymax=-1　D.T=2，ymax=-1

7.将函数f（x）=sin x的图像向右平移φ（0≤φ≤2π）个单位后，得到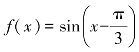的图像，则φ=（　）.

三、解答题

1.求函数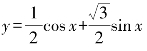的周期、最大值、最小值.

2.已知sin x=，若x∈［0，2π），求x的值.

一、填空题

1.函数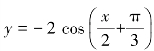的最小正周期是__________，最大值为__________，最小值为________.

2.函数y=cos22x-sin22x的最小正周期是________，最大值为________，最小值为________.

3.函数y=-sin x cos x的最小正周期是________，最大值为________，最小值为________.

4.函数y=的最小正周期是________，最大值为________，最小值为________.

5.函数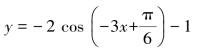的最小正周期是________，最大值为________，最小值为________.

6.已知f（x）=ax+b sin x+1，若f（5）=7，则f（-5）=________.

7.已知，当x∈［0，π］时，则x=________；当x∈［0，2π）时，则x=________.

8.已知，当x∈［0，2π）时，则x=________.

9.已知函数f（x）=3 sin 2x+4 cos 2x，则该函数的最大值为________.

10.函数的周期是________，振幅是________.

11.已知tan α=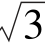，且若α∈［0，2π），则α=________.

二、选择题

1.下列不等式成立的是（　）.

2.已知函数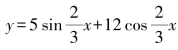，x∈R，用T表示它的最小正周期，P表示它的值域，下列结论正确的是（　）.

A.T=2π，P=［-1，1］　B.T=3π，P=［-13，13］

C.T=π，P=［5，12］　D.T=π，P=R

3.在下列函数中，最小正周期为4π的是（　）.

A.y=sin　B.y=sin x　C.y=sin 2x　D.y=sin 4x

4.函数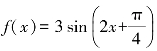的最小正周期和最大值分别是（　）.

5.将函数f（x）=3 sin 2x的图像向左平移φ（0≤φ≤2π）个单位后，得到f（x）=3 sin的图像，则φ=（　）.

三、解答题

1.求函数y=sin（x+11π）cos（x+7π）的最小正周期.

2.已知函数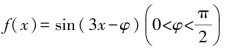，（1）求f（x）的最小正周期；（2）若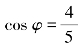，求的值。

3.已知函数，求它的定义域.

1.已知函数f（x）=-1+2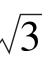sin x cos x+2 cos2x，

（1）求f（x）的最小正周期；

（2）求f（x）的单调递减区间；

（3）当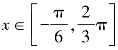时，求f（x）的最大值和最小值.

2.函数y=11-8 cos x-2 sin2x，（1）当x为何值时，y有最大值是多少？（2）当x为何值时，y有最小值是多少？

解三角形

考纲内容：正弦定理、余弦定理、三角形面积公式.

考纲要求：掌握用正弦定理、余弦定理、三角形面积公式进行计算和解决简单的实际问题.