中职数学升学考试教程：第四节，和差倍角公式

考点剖析：掌握两角和差及二倍角的正弦、余弦、正切公式，并能用公式完成简单三角函数式的恒等变形.

1.两角和与差的三角函数公式

（1）sin（α+β）=sin α cos β+cos α sin βsin（α-β）=sin α cos β-cos α sin β

（2）cos（α+β）=cos α cos β-sin α sin βcos（α-β）=cos α cos β+sin α sin β

（3）tan（α+β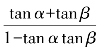）=　tan（α-β）=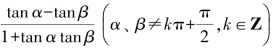

2.二倍角的三角函数公式

（1）sin 2α=2 sin α cos α

（2）cos 2α=cos2α-sin2α=2 cos2α-1=1-2 sin2α

（3）tan 2α=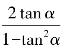（二倍角公式是利用和角公式由2α=α+α推导而得）

3.利用和、差、倍角公式计算和恒等变形时，常常用角的变化进行解答.例如：15°=60°-45°=45°-30°，75°=45°+30°，105°=60°+45°，120°=2×60°，（α+β）-β=α，（α+β）-（α-β）=2β等.　

【题型1】利用和、差、倍角公式求值

例1　sin 58°cos 28°-cos 58°sin 28°=________________________________________，

=_________________________________________，

cos 25°cos 20°-sin 25°sin 20°=_________________________________________，

=____________，=__________，=____________.

解：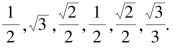

例2　判断tan 135°=tan（90°+45°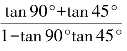）=分解是否正确.

解：不正确.因为tan 90°没有意义，它只能利用诱导公式来求解：

tan 135°=tan（90°+45°）=-cot 45°=-1

或tan 135°=tan（180°-45°）=-tan 45°=-1

【锦囊妙计】两角和与差的三角函数公式可借助口诀：s→s，c，c，s符号不变，c→c，c，s，s符号要变，t→t，t，1，tt下变上不变.

赢在起点

1.cos 50°cos 5°+sin 50°sin 5°=________________________________________，

=____________；sin 15°cos 105°+cos 15°sin 105°=____________.

2.（2013年高考题）　2 sin 30°cos 30°=____________，2 cos2 -1=__________；若tan α=2，则tan 2α=____________.

【题型2】求15°、75°、105°的三角函数值

例1　求cos 15°的值.

解：cos 15°=cos（60°-45°）=cos 60°cos 45°+sin 60°sin 45°

=

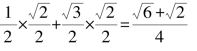
例2　求tan 75°的值.

解：tan 75°=tan（45°+30°）=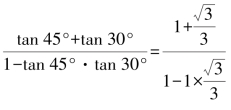

=

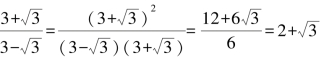
【锦囊妙计】常见的几个函数值：

tan 75°=cot 15°=2+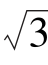，tan 15°=cot 75°=2-.

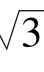赢在起点

sin 15°=__________，sin 75°=__________，sin 105°=__________，

sin 165°=__________；cos 15°=__________，cos 75°=__________，

cos 105°=__________，cos 165°=__________；tan 15°=__________，

tan 75°=__________，tan 105°=__________，tan 165°=__________.

【题型3】和、差、倍角公式的综合应用

例1　已知，且，求sin 2α，cos的值.

解：因为sin2α+cos2α=1且

所以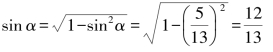

sin 2α=2 sin α cos α=

例2　已知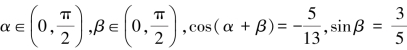，求sin α的值.

解：因为sin2（α+β）+cos2（α+β）=1，且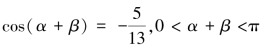

所以sin（α+β）=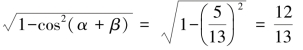

又因为sin2β+cos2β=1且

所以cos β=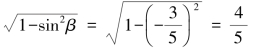

sin α=sin［（α+β）-β］=sin（α+β）cos β-cos（α+β）sin β

=

【锦囊妙计】解决三角变换问题应认真分析已知角和所求角的关系，考虑角的整体运用.常见的拼角和拆角如下：

2α=（α+β）+（α-β），2β=（α+β）-（α-β），α=（α+β）-β，α=（α-β）+β，β=（α+β）-α，

β=-（α-β）+α，2α+β=2（α+β）-β，2α-β=2（α-β）+β.

例3　已知：tan α，tan β是方程的x2+3x-5=0两个实根，tan（α+β）的值.

解：由题意可得　tan α+tan β=-3，tan α·tan β=-5，

赢在起点

1.已知，且，则cos α=________，sin 2α=________，cos 2α=________，tan 2α=________，=__________.

2.已知，且0＜β＜α＜，则α-β是第____象限的角，sin（α-β）=__________；由β=α-（α-β）得cos β=__________.

【题型4】证明三角函数恒等式

例　求证

证明：左边=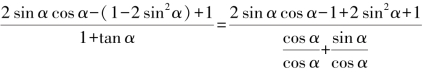

=

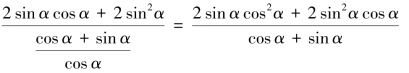
==2 sin α cos α=sin 2α=右边

所以原等式成立.

【锦囊妙计】化简三角函数式的要求：①能求出值的要求出值；②三角函数式的项数、三角函数及角的种类尽可能少；③三角函数式的次数尽可能低；④分母中尽量不含三角函数式和根式.

证明三角函数恒等式的技巧：由繁到简，正用、逆用公式，切化弦，高次化低次，异角化同角，异名化同名，巧用数字“1”.

赢在起点

求证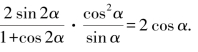

一、填空题

1.sin 26°cos 34°+cos 26°sin 34°=_________________，2 sin 15°cos 15°=________________，

cos 82°cos 22°+sin 82°sin 22°=________________，2 cos2-1=________________，

cos 40°sin 20°+cos 20°sin 40°=____________，2 cos 22.5°sin 22.5°=____________，

1-2 sin215°=________________，=________________，(https://www.xing528.com)

sin=________________，=________________.

2.sin 15°=____________，cos 75°=____________，tan 105°=____________，

sin 165°=____________，cos 105°=____________，tan 15°=____________.

3.=____________，=____________.

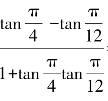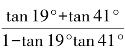4.若sin α=，则cos 2α=________，若tan α=5，则tan 2α=____________.

二、选择题

1.sin 105°的值是（　）.

2.tan 75°=（　）.

3.已知tan α=2，tan β=，则tan（α-β）=（　）.

4.cos 4α-sin 4α可化简为（　）.

A.cos 4α　B.cos 2α　C.1　D.sin 2α

5.=（　）.

一、填空题

1.若，则sin 2α=________，cos 2α=________，tan 2α=________.

2.=________.

3.sin 15°sin 75°=____________，=____________.

4.=____________，=____________，=____________.

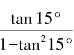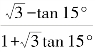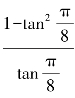5.若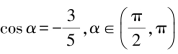，则=____________.

6.化简=____________.

7.化简f（x）=（sin x+cos x）2+1=________________.

8.化简f（x）=1-2 cos2x=________________.

9.若sin α+cos α=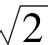，则sin 2α=________________.

10.已知P（-3，4）是角α的终边上的一点，则cos 2α的值为____________________.

二、选择题

1.已知α、β均为锐角，且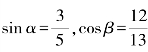，则sin（α-β）=（　）.

2.sin 14°cos 16°+sin 76°cos 74°的值是（　）.

3.若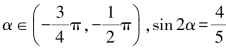，则cos α=（　）.

4.sin 15°·sin 30°·sin 75°的值等于（　）.

5.（2013年高考题）已知，则sin4α-cos4α可化简为（　）.

三、解答题

1.计算

2.已知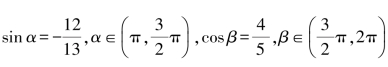，求cos（α-β）的值.

3.证明sin（2α+β）-2 sin α·cos（α+β）=sin β.

4.证明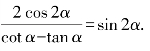

5.证明三角恒等式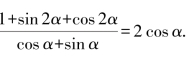

6.已知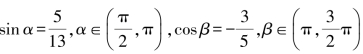：，求tan（α+β）的值.

7.证明当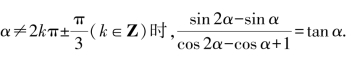

1.已知，（1+tan α）（1+tan β）=（　）.

A.-1　B.1　C.-2　D.2

2.已知，求cos 2α的值.

3.已知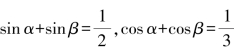，求cos（α-β）的值.

4.已知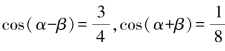，求tan α tan β的值.

5.已知α，β为锐角，且tan α、tan β是方程x2-3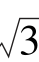x+4=0的两个根，求：

（1）（1+tan α）（1+tan β）的值；

（2）α+β的度数.

自我评价

（满分100分，时间45分钟）　评价结果：__________

一、填空题（每题5分，共50分）

1.sin 15°=________________.

2.cos 105°=________________.

3.sin 22.5°cos 22.5°=________________.

4.若，则cos 2α=________________.

5.sin 87°cos 27°-cos 87°sin 27°=________________.

6.cos 115°cos 5°-sin 115°sin 5°=________________.

7.若cos（π-α）=，则cos（-α）=________________.

8.若tan α=2，tan β=3，则tan（α+β）=________________.

9.若=________________.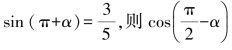

10.若，则（sin α-cos α）2=________________.

二、选择题（每题5分，共20分）

1.下列等式正确的是（　）.

A.若sin α=，则sin 2α=　B.sin（α+β）=sin α+sin β

C.若sin α=，则α=30°　D.当时，tan（α-β）=

2.sin 240°=（　）.

3.已知A（3，-4）是角α的终边上的一点，则sin 2α的值为（　）.

4.若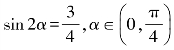，则sin α-cos α=（　）.

三、解答题（每题10分，共30分）

1.若的值.

2.若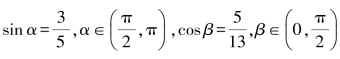，求cos（α+β）的值.

3.求证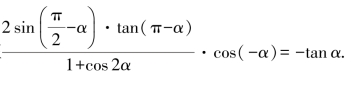

三角函数的图像和性质

考纲内容：正弦函数、余弦函数的图像和性质、正弦型函数y=A sin（ωx+φ）的概念与图像；已知三角函数值求角.

考纲要求：了解正弦函数、余弦函数、正弦型函数的概念和图像；理解正、余弦函数的性质；会求正弦型函数y=A sin（ωx+φ）的最值和周期；能根据已知正、余弦函数值求［0，2π）上的特殊角；能解决简单的三角函数问题.