考点剖析:掌握用诱导公式进行求值、化简和证明.
1.诱导公式是把任意角的正弦、余弦、正切、余切转化为锐角的正弦、余弦、正切、余切,从而求出相应的函数值.
2.诱导公式表:
注:上述诱导公式的记忆方法:可借“纵变横不变,符号看象限”或“奇变偶不变,符号看象限”理解记忆;把α形式地看成为锐角.
【题型1】利用诱导公式求值
例1 计算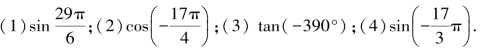
解:(1)![]()
(2)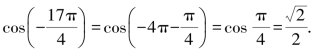
(3)![]()
(4)![]()
例2 已知![]() ,则cos α的值是( ).
,则cos α的值是( ).
解: D.
赢在起点
1.求下列各式的值: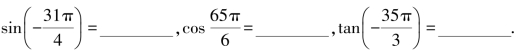
2.已知![]() ,则
,则![]() =____________.
=____________.
【题型2】用诱导公式化简、证明
例1 化简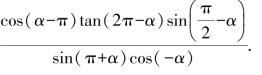
解:原式![]()
=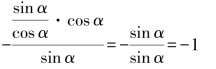
例2 求证
证明:左边![]()
=![]()
所以原等式成立.
赢在起点
1.已知角α终边经过点P(3,-4),则sin α=_______,cos α=_______,tan α=________,sin(π+α)=________,cos(π+α)=________,tan(2π-α)=________.
2.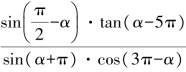 =____________.
=____________.
一、填空题
1.cos(-α)=________,sin(π+α)=________,tan(π-α)=________,
sin(2π-α)=________,![]() =________,
=________,![]() =________,
=________,
cos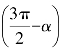 =________,
=________,![]() =________.
=________.
2.sin 30°=________,tan 45°=________,cos![]() =________,sin
=________,sin![]() =________,
=________,
tan 60°=________,cos(-45°)=________,sin(-30°)=________,tan![]() =________,
=________,
sin(-45°)=________,tan 150°=________,sin 240°=________,tan(-135°)=________,
cos 180°=________,tan ![]() π=________,sin 150°=________,tan 225°=________,(https://www.xing528.com)
π=________,sin 150°=________,tan 225°=________,(https://www.xing528.com)
cos 330°=________,cos ![]() =________,tan
=________,tan ![]() =________,cos
=________,cos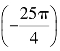 =________,
=________,
sin![]() =________.
=________.
3.![]() =________.
=________.
二、选择题
1.sin 750°=( ).
2.cos![]() =( ).
=( ).
3.tan 315°=( ).
4.下列各式中与cos α相等的是( ).
A.cos(π-α) B.sin(2π-α) C.sin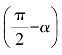 D.cos
D.cos![]()
一、填空题
1.sin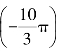 =________,tan 330°=________.
=________,tan 330°=________.
2.若![]() ,则
,则![]() =________,若tan(π-α)=-2,则tan(2π-α)=________.
=________,若tan(π-α)=-2,则tan(2π-α)=________.
3.若tan(6π-α)=-7,则tan(-3π+α)=________.
4.cos228°+tan 33°·tan 57°·cot 45°+cos262°=________.
5.![]() =________.
=________.
6.sin21°+sin22°+sin23°+…+sin288°+sin289°=________.
7.tan 26°·tan 64°=________,sin2 10°+sin2 80°=________.
二、选择题
1.已知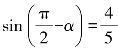 ,则cos(π-α)的值是( ).
,则cos(π-α)的值是( ).
2.cos 225°+tan 240°+sin(-60°)=( ).
3.如果![]() ,那么cos(π-α)=( ).
,那么cos(π-α)=( ).
4.tan(π+α)·cos(-α)-sin(8π+α)=( ).
A.2 sin α B.0 C.-2 sin α D.cos α
三、解答题
1.已知:cos(π+α)=![]() ,α为第三象限的角,求sin α,tan α的值.
,α为第三象限的角,求sin α,tan α的值.
2.已知sin α和cos α是方程5x2-x+m=0的两实根,求m的值.
3.化简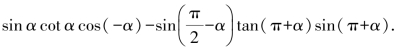
4.已知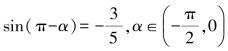 ,求cos(π+α)的值.
,求cos(π+α)的值.
1.已知cos 31°=m,则sin 239°·tan 149°=( ).
2.化简cos 1°+cos 2°+cos 3°+…+cos 179°+cos 180°.
3.化简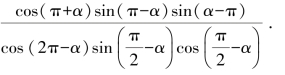
4.求证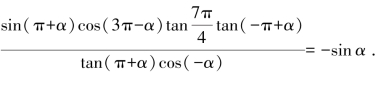
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




