数学教程：学习平移的定义及变化规律

考点剖析：了解平面内点平移、图像平移的变化规律，会用平移变化规律研究函数图像及性质；根据函数解析式明确图像的变化过程，熟练运用平移找出平移前（或后）函数的解析式.

1.平移的定义：把平面内（或空间里）每个点按照同一个方向移动相同的距离，称为平面（或空间）的一个平移.

2.变换（h＞0，k＞0）

（1）点的对称：在平面直角坐标Oxy内任取一点P（a，b），它

①关于x轴对称，得到点P′的坐标为（a，-b）；

②关于y轴对称，得到点P″的坐标为（-a，b）；

③关于直线y=x对称，得到点P‴的坐标为（b，a）；

④关于直线y=-x对称，得到点P″″的坐标为P（-b，-a）.

（2）点的平移：在平面直角坐标Oxy内任取一点P（a，b），它

①向左平移h个单位，得到点P′（a-h，b）；

②向右平移h个单位，得到点P″（a+h，b）；

③向上平移k个单位，得到点P‴（a，b+k）；

④向下平移k个单位，得到点P″″（a，b-k）.

（3）图像的平移：在平面直角坐标Oxy内，若函数f（x）的图像是E，把图像

①向左平移h个单位，得到图像E′的函数解析式为f（x+h）；

②向右平移h个单位，得到图像E″的函数解析式为f（x-h）；

③向上平移k个单位，得到图像E‴的函数解析式为f（x）+k；

④向下平移k个单位，得到图像E″″的函数解析式为f（x）-k.

【锦囊妙计】点平移口诀：“左减右加，下减上加”，图像平移口诀：“左加右减，上加下减”.

【题型1】求对称点的坐标

例　在平面上建立一个直角坐标Oxy，点（2，3）关于x轴、y轴、直线y=x的对称点的坐标分别为____________、____________、____________.

解：（2，-3）、（-2，3）、（3，2）.

赢在起点

在平面直角坐标Oxy内，点（-3，1）关于x轴的对称点的坐标为________，关于y轴的对称点的坐标为____________，关于直线y=-x的对称点为____________.

【题型2】求平移前（后）函数的解析式

例1　在平面上建立一个直角坐标Oxy，在平面上任取一点P（a，b），则

（1）向左平移2个单位后，得到点P′的坐标为________________；

（2）向右平移2个单位后，得到点P″的坐标为________________；

（3）向上平移2个单位后，得到点P‴的坐标为________________；

（4）向下平移2个单位后，得到点P″″的坐标为_________________.

例2　在平面上建立一个直角坐标Oxy，向右平移3个单位，点P（2，1）、Q（-1，5）、M（0，-4）的像P′，Q′，M′的坐标分别是多少？

解：1.（1）（a-2，b），（2）（a+2，b），（3）（a，b+2），（4）P（a，b-2）.

2.P′（5，1），Q′（2，5），M′（3，-4）.

例3　函数的图像E向左平移1个单位后的像是E′，再向下平移3个单位后得图像E″，如图所示，请分别写出E′，E″所表示的函数解析式.

解：如图所示，函数向左平移1个单位后得到y=，再向下平移3个单位后得到

赢在起点

1.在平面上建立一个直角坐标Oxy，点（2，3）经过向________平移________个单位得到点（-1，3），再经过向________平移________个单位得到点（-1，5）.

2.函数y=2x向右平移3个单位后得到函数____________，再向上平移2个单位后得到函数____________.

3.函数y=2（x+2）2-3是由函数y=2x2经过怎样变化得到的？

4.请画出函数的大致图像.

一、填空题

1.在平面上建立一个直角坐标系Oxy，向右平移2个单位，则

（1）点（-3，1）平移后的坐标是__________；

（2）点（3，1）平移后的坐标是__________；

（3）点（-3，-1）平移后的坐标是__________；

（4）点（3，-1）平移后的坐标是__________.

2.在平面上建立一个直角坐标系Oxy，点（-2，3）关于x轴的对称点的坐标为____________，点（1，-4）关于y轴的对称点的坐标为____________，点（m，n）关于直线y=x的对称点的坐标为____________.

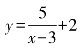3.函数的图像向______平移______个单位，再向______平移______个单位得到函数的图像.

4.函数y=x2的图像向______平移______个单位得到函数y=（x+2）2的图像，再向______平移______个单位得到函数y=（x+2）2-3的图像.

5.函数y=2x2+3的图像向______平移______个单位得到函数y=2（x+1）2+3的图像.

6.函数y=ax-1+2的图像是由函数y=ax的图像上所有的点经过怎样的变化得到的图像？________________________________.

7.函数y=2 sin x的图像经过向左平移个单位，再向上平移2个单位后得到的函数图像的解析式为____________.

二、选择题

1.点（a，b）关于y轴对称的点的坐标为（　）.

A.（a，b）　B.（-a，b）　C.（a，-b）　D.（-a，-b）

2.将点（3，-2）先向右平移2个单位，再向上平移3个单位得到点（　）.

A.（5，1）　B.（1，1）　C.（5，-5）　D.（1，5）

3.函数y=2x的图像先向右平移2个单位，再向下平移1个单位得到函数的解析式为（　）.

A.y=2x-2-1　B.y=2x-2+1　C.y=2x+2-1　D.y=2x+2+1

4.为了得到函数y=log2（x+1）-2的图像，只需要把函数y=log2x的图像上所有的点（　）.

A.向左平移1个单位，再向上平移2个单位

B.向左平移1个单位，再向下平移2个单位

C.向右平移1个单位，再向上平移2个单位

D.向右平移1个单位，再向下平移2个单位(www.xing528.com)

5.若关于x的函数y=ax+b的图像如右图所示，则（　）.

A.0＜a＜1，b＜0　B.0＜a＜1，b＞0

C.a＞1，b＜0　D.a＞1，b＞0

一、填空题

1.点（3，-2）关于直线y=x的对称点的坐标为____________.

2.函数y=2x2的图像经过先向左平移1个单位，再向上平移3个单位得到的图像的解析式为_________________.

3.函数y=3x2-6x+2的图像是由函数y=3x2的图像经过先向______平移______个单位，再向______平移______个单位得到的.

4.函数y=log3（-2x）的图像经过向左平移3个单位，再向上平移2个单位得到的图像的解析式为______________.

5.函数y=3 cos 2x的图像向右平移个单位后得到的图像的解析式为____________.

二、选择题

1.点（m，n）关于直线x=1的对称点是（　）.

A.（2-m，n）　B.（m+1，n）　C.（m，2-n）　D.（m，n-1）

2.为了得到函数的图像，只需把函数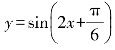的图像（　）.

A.向左平移个单位　B.向右平移个单位

C.向左平移个单位　D.向右平移个单位

3.若关于x的函数y=ax-b的图像如右图所示，则（　）.

A.0＜a＜1，b＜0　B.0＜a＜1，b＞0

C.a＞1，b＜0　D.a＞1，b＞0

4.若关于x的函数的图像如右图所示，则函数的解析式为（　）.

A.y=　B.y=

C.y=　D.y=

三、解答题

1.已知函数的图像是由函数y=3 sin 2x的图像向左平移φ（φ＞0）个单位后得到的图像，求φ的值.

2.求函数y=log3（2x2+x）的图像向右平移个单位后得到的函数图像的解析式.

1.求函数的图像是由函数y=sin 2x的图像经过怎样的变化得到的.

2.为了得到函数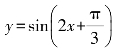的图像，只需将函数y=sin 2x的图像（　）.

A.向左平移个单位　B.向右平移个单位

C.向左平移个单位　D.向右平移个单位

自我评价

（满分100分，时间45分钟）　评价结果：__________

一、填空题（每题5分，共50分）

1.log 28=________________.

2.=_________________.

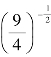3.已知2 log6x=1-log63，则x的值是________________.

4.若f（x）=log3（x-1），且f（a）=2，则a=________________.

5.指数函数必过定点________________，对数函数必过定点________________.

6.函数f（x）=lg（2-x2）的定义域是________________.

7.若loga2＞loga1，那么a的取值范围是________________.

8.如果函数f（x）=（a-1）x在R上是减函数，那么实数a的取值范围是____________.

9.函数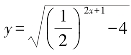的定义域是____________.

10.已知幂函数过点（2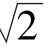，），则函数的解析式为____________.

二、选择题（每题5分，共25分）

1.下列4个式子（其中a＞0且a≠1，M＞0，N＞0）中正确的有（　）.

（1）logaM+logaN=loga（MN）　（2）logaM-logaN=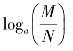

（3）loga（M-N）=　（4）

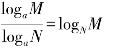
A.1个　B.2个　C.3个　D.4个

2.已知x-3=8，那么x等于（　）.

A.2　B.-2　C.±2　D.

3.60.7，0.76，log0.76的大小顺序是（　）.

A.0.76＜log0.76＜60.7　B.0.76＜60.7＜log0.76

C.log0.76＜0.76＜60.7　D.log0.76＜60.7＜0.76

4.若，则m，n的关系正确的是（　）.

A.m =　B.m=n　C.m＞n　D.m＜n

5.若关于x的函数y=ax+b的图像如右图所示，则（　）.

A.0＜a＜1，b＜0　B.0＜a＜1，b＞0

C.a＞1，b＜0　D.a＞1，b＞0

三、解答题（每题10分，共30分）

1.指数函数f（x）=ax的图像过点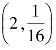，求f（0），f（1），f（-2）.

2.解对数方程log2（x2-5x-2）=2.

3.已知函数f（x）=log0.2（2x2+3x+1），

（1）求这个函数的定义域；

（2）当x取何值时，f（x）≥0？