考点剖析:理解指数与对数的概念、运算法则;了解指数与对数的互化;了解分数指数幂的概念;识记指数与对数的运算法则,能用指数和对数运算法则及公式进行简单运算.
1.指数幂
(1)![]() ,其中a为底数,n为指数,an称为a的n次幂;
,其中a为底数,n为指数,an称为a的n次幂;
(2)当a≠0时,![]() ,a0=1,(n∈N*);
,a0=1,(n∈N*);
(3)![]() ,(当n为偶数且m为奇数时,a≥0;当n为奇数时,a∈R).
,(当n为偶数且m为奇数时,a≥0;当n为奇数时,a∈R).
2.指数的运算法则
设a>0,b>0,x、y∈R,则
(1)ax·ay=ax+y,(2)ax÷ay=ax-y,(3)(ax)y=axy,(4)(ab)x=ax·bx.
3.指数和对数的转化
当a>0,a≠1时,ab=N⇔logaN=b(N>0).
注:①0和负数没有对数;②log10N=lg N;③logeN=ln N.
4.对数的运算公式及法则
设a>0,a≠1,b>0,b≠1,M>0,N>0,则
(1)loga1=0,(2)logaa=1,
(3)![]() =N,(4)logaan=n,
=N,(4)logaan=n,
(5)logaM+logaN=loga(M·N),(6)logaM-logaN=![]() ,
,
(7)logaMn=n logaM,(8)logab·logba=1,
(9)logbN=![]() (换底公式).
(换底公式).
【题型1】根式与分数指数幂、对数与指数的互化
例1 根式与分数指数幂互化
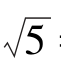 =________,
=________,![]() =________,
=________,![]() =________,
=________,![]() =________.
=________.
例2 指数与对数互化
23=8⇔__________,![]() ⇔__________,log5125=3⇔__________,
⇔__________,log5125=3⇔__________,
![]() =-3⇔__________.
=-3⇔__________.
赢在起点
1.将下列根式与分数指数幂进行互化、对数与指数进行互化.
![]() =________,
=________,![]() =________,
=________,![]() =__________,
=__________,
63=216⇔______________,log3![]() =-2⇔____________.
=-2⇔____________.
2.下列等式成立的是( ).
A.![]() B.
B.![]()
C.2-3=![]() D.
D.![]()
【题型2】基本公式的应用
例 (1)设m,n为不等于1的两个正数,则下列等式成立的是( ).
A.elg mn=mn B.(3n)m=3mn
C.![]() =lg(m-n) D.logmn=lognm
=lg(m-n) D.logmn=lognm
(2)下列命题或运算中,正确的是( ).
A.若4x=10,则x=log104 B.若log4x=10,则4x=10
C.![]() D.
D.
(3)下列运算中正确的是( ).
A.log23·log25=log215 B.log23·log25=log28
C.![]() =log53 D.
=log53 D.![]()
(4)下列运算中正确的是( ).
A.(-1)0=-1 B.![]()
C.(53)2·54=59 D.![]()
解:(1)B; (2)C; (3)C; (4) B.
赢在起点
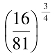 =___________,(2ab2)3=________,
=___________,(2ab2)3=________,![]() =__________,
=__________,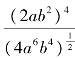 =____________,(
=____________,(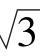 -1)4·(1+
-1)4·(1+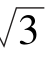 )4=________,(
)4=________,(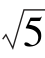 -π)0=________,5log53=____________,log28=___________,log48=__________,lg 0.0001=____________,log99(
-π)0=________,5log53=____________,log28=___________,log48=__________,lg 0.0001=____________,log99( -
-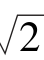 )0=____________,log21 3+log21 7=____________,lg 80-lg 8=____________,log45·log254=________.
)0=____________,log21 3+log21 7=____________,lg 80-lg 8=____________,log45·log254=________.
【题型3】指数、对数等的综合运算
例 计算:(1)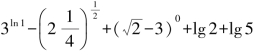
解:原式=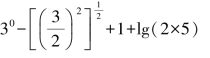
=![]()
=![]() (https://www.xing528.com)
(https://www.xing528.com)
(2)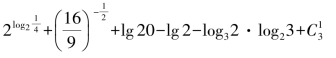
解:原式=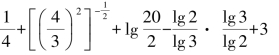
=![]()
(3)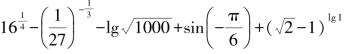
解:原式=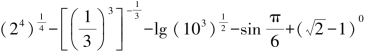
=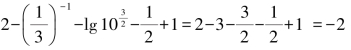
赢在起点
1.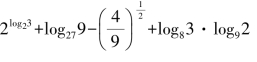
2.2ln 1+lg 0.001![]()
3.log24+2-1-![]()
一、填空题
1.(1)根式![]() 化成分数指数幂为__________,分数指数幂
化成分数指数幂为__________,分数指数幂![]() 化成根式为__________.
化成根式为__________.
(2)指数式23=8化成对数式为__________,对数式log327=3化成指数式为________.
(3)(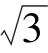 +1)0=____________,
+1)0=____________,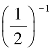 =__________,
=__________,![]() =__________.
=__________.
2.(1)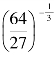 =____________;(2)
=____________;(2)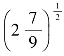 =____________;(3)
=____________;(3)![]() =____________;
=____________;
(4)(-a3)2=____________;(5)![]() =____________;(6)log3
=____________;(6)log3![]() =____________;
=____________;
(7)log3( -1)0=____________;(8)log43·log34=____________;
-1)0=____________;(8)log43·log34=____________;
(9)log315-log35=____________;(10)log64+log69=____________.
二、选择题
1.log2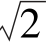 的值为( ).
的值为( ).
A.-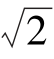 B.
B.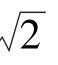 C.
C.![]() D.
D.![]()
2.2-3=![]() 化为对数式为( ).
化为对数式为( ).
A.![]() =-3 B.
=-3 B.![]() (-3)=2 C.log2
(-3)=2 C.log2![]() =-3 D.log2(-3)=
=-3 D.log2(-3)=![]()
3.计算log93+log927=( ).
A.1 B.2 C.3 D.4
一、填空题
(1)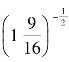 =____________;(2)log2
=____________;(2)log2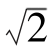 =________;
=________;
(3)若log2x=3,则x=____________;(4)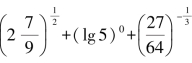 =____________;
=____________;
(5)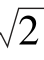 ·
·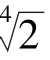 ·
· =________;(6)若3a=2,3b=5,则32a-b=____________;
=________;(6)若3a=2,3b=5,则32a-b=____________;
(7)log89·log2732=____________;(8)log225·log38·log59=____________.
二、选择题
1.计算log43·log916=( ).
A.1 B.![]() C.log34 D.log32
C.log34 D.log32
2.若log34=m,则log43=( ).
A.![]() B.m C.m-1 D.1-m
B.m C.m-1 D.1-m
3.![]() =( ).
=( ).
A.2 B.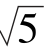 C.5 D.25
C.5 D.25
三、解答题
1.计算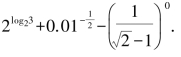
2.计算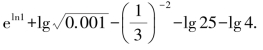
3.计算lg 5+sin2(-45°)+lg 2+log56·log625+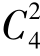 .
.
4.计算![]()
5.计算lg 5+lg 2+tan![]()
1.若log123=m,则log124=( ).
A.![]() B.m+1 C.m-1 D.1-m
B.m+1 C.m-1 D.1-m
2.![]() =( ).
=( ).
A.5 B.2 C.10 D.25
3.(2013年高考题)计算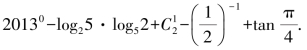
4.(2014年高考题)计算log39+23+sin![]()
5.(2015年高考题)计算50+lg 100-tan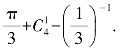
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




