简单函数图像性质及应用

考点剖析：理解一元二次函数的图像和性质；了解用待定系数法求一次函数和二次函数的解析式；了解对常见函数图像的识别方法，会建立简单的函数关系；掌握用二次函数求最大面积或最大利润，掌握用函数、方程、不等式的知识解决有关简单实际问题.

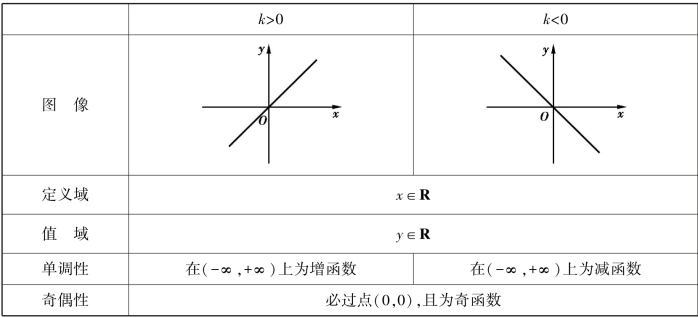
1.正比例函数的定义、图像和性质

（1）如果y=kx（k为常数，k≠0），则称y为x的正比例函数.

（2）正比例函数的图像和性质如下表：

2.反比例函数的定义、图像和性质

（1）如果y=（k为常数，k≠0），则称y为x的反比例函数.

（2）反比例函数的图像和性质如下表：

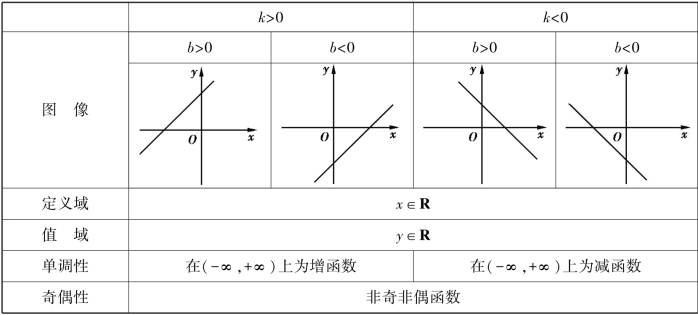
3.一次函数的定义、图像和性质

（1）如果y=kx+b（k、b均为常数，k≠0），则称y为x的一次函数（正比例函数是一次函数b=0时的特殊情形）.

（2）一次函数的图像和性质如下表：

4.二次函数的3种表示

（1）一般式：y=ax2+bx+c（a≠0）；

（2）顶点式：y=a（x-h）2+k，其中（h，k）为抛物线的顶点；

（3）截距式（交点式）：y=a（x-x1）（x-x2），其中x1、x2为抛物线与x轴交点的横坐标.

5.二次函数y=ax2+bx+c的图像为抛物线，其图像及性质如下表：

注：①当Δ=b2-4ac＞0时，抛物线与x轴有两个交点，交点横坐标为方程ax2+bx+c=0的两个实数根；
②当Δ=b2-4ac=0时，抛物线与x轴有且只有一个交点，交点横坐标为方程ax2+bx+c=0的一个实数根；
③当Δ=b2-4ac＜0时，抛物线与x轴没有交点，方程ax2+bx+c=0无实数根；
④抛物线与y轴交点为（0，c）.

【题型1】用待定系数法求函数解析式

例1　已知一次函数f（x）过点（1，1），（2，-1），求函数f（x）的解析式.

解：设一次函数的解析式为f（x）=kx+b

因为函数图像过点（1，1），（2，-1）

则

解得

所以一次函数的解析式为　f（x）=-2x+3.

例2　已知二次函数f（x）满足f（0）=0，f（1）=f（-1）=2，求函数f（x）的解析式.

解法1：设二次函数的解析式为f（x）=ax2+bx+c（a≠0），

由f（0）=0，f（1）=f（-1）=2得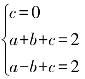

解得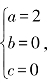

所以二次函数的解析式为f（x）=2x2.

解法2：由题可知二次函数的对称轴为x=0，顶点坐标为（0，0），

设二次函数的解析式为f（x）=ax2（a≠0），

由f（1）=2得a=2，

所以二次函数的解析式为f（x）=2x2.

赢在起点

1.已知抛物线f（x）=ax2+bx+c（a≠0）的顶点坐标为（1，-2），且过（2，1），求抛物线的方程.

2.已知二次函数过（-2，0），（3，0），（1，6），求二次函数的解析式.

【题型2】根据图像判断系数符号

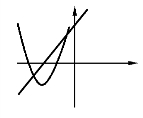
例　已知二次函数y=ax2+bx+c（a≠0）的图像如图所示，试判断a，b，c的符号.

解：（如图）因为抛物线开口向下，所以a＜0，

因为对称轴在y轴右边，所以＞0，即b＞0，

因为抛物线与y轴交与正半轴，所以c＞0，

即a＜0，b＞0，c＞0.

赢在起点

1.已知二次函数y=ax2+bx+c（a≠0）的图像如右上图所示，试判断a，b，c的符号正确的是（　）.

A.a＞0，b＞0，c＞0　B.a＜0，b＜0，c＜0

C.a＜0，b＞0，c＞0　D.a＜0，b＜0，c＞0

2.下列表示函数f（x）=ax+b与f（x）=ax2+bx+c（a≠0）的图像正确的是（　）.

A.　

B.　

C.　

D.

【题型3】一元二次函数的实际应用

例1　已知二次函数y=-x2+2（m-1）x-m2+2m，

（1）当函数图像经过原点时，求m的值；

（2）证明：无论m取何实数，二次函数的图像与x轴总有两个交点.

解：（1）因为函数图像经过原点

-m2+2m=0　即m=0或m=2

（2）对一元二次方程-x2+2（m-1）x-m2+2m=0

因为Δ=［2（m-1）］2-4×（-1）×（-m2+2m）

=4m2-8m+4-4m2+8m

=4＞0

所以方程有两个不相等实数根

故二次函数图像与x轴总有两个交点.

例2　某商店购进一批女式T恤，进价50元/件，若按50元/件销售，每月可售100件，若每件每增加1元销售，每月销售量也减少一件，另外商店每月还需支付其他费用900元，问：每件的售价应定在什么范围，才使得商店不亏本？

解：设每件T恤的价格为x元，利润为y元

则y=（x-50）［100-（x-50）］-900

=-x2+200x-8400（50≤x≤150）

要使得不亏本，则y≥0，即-x2+200x-8400≥0⇔60≤x≤140

答：每件的售价应定在60～140元，才使得商店不亏本.

例3　用长16 m的铝材做一个目字形窗框，试问：高和宽各为多少米时窗户的透光面积最大？最大面积是多少？

解：设目字形窗框的宽为x m，则窗框的高为，设透光面积为S m2，由题意得：

S=x·=-2x2+8x

=-2（x-2）2+8　（0＜x＜4）

因为-2＜0，所以当x=2，=4时，Smax=8.

所以当目字形窗框的宽为2 m，窗框的高为4 m时，最大透光面积为8 m2.

【锦囊妙计】当矩形的周长一定时，表示它的面积的关键是正确表示矩形的长与宽.

例4　某超市购进一批20元/kg的绿色食品，如果以30元／kg销售，那么每天可售出400 kg，由销售经验知，每天销售量y（kg）与销售单价x（元）（x≥30）存在如右图所示的一次函数关系式.

（1）试求出y与x的函数关系式；

（2）设该超市销售绿色食品每天获得利润P元，当销售单价为何值，每天可获得最大利润？最大利润是多少？

解：（1）设y=kx+b，由图像可知，

即一次函数关系式为y=-20x+1000（30≤x≤50）.

（2）P=（x-20）·y=（x-20）（-20x+1000）

=-20x2+1400x-20 000

=-20（x-35）2+4500

因为-20＜0，所以当x=35时，Pmax=4500（元）.

所以当销售单价35元时，每天可获得最大利润，最大利润是4500元.

赢在起点

1.水渠的横截面为等腰梯形，它的周长为6 m，如图所示，设在梯形ABCD中，∠C=60°，记BC=x，求梯形的腰长x为何值时，水渠流量最大？此时水渠的横截面面积为多少？

解：设梯形面积用y表示，由题意得=________米，=________米，=________米，=________米，由梯形面积公式________________，得y=________________，x的取值范围是____________________，这是一个一元二次函数，因为a=____________＜0，所以当x=________时，ymax=________平方米.故梯形的腰长为________米时，水渠流量最大，此时水渠的横截面面积为____________平方米.

2.某件商品的进价为40元，售价为每件50元，每个月可卖出210件，如果每件商品的价格每上涨1元，每个月将少卖出10件（每件不高于65元）.设每件商品的售价上涨x元（x为整数），每个月的销售利润为y元.

（1）求y与x的函数关系式，并直接写出自变量x的取值范围；

（2）若每个月的利润为2200元，求每件商品的售价应定为多少元？

（3）每件商品的售价应定为多少元时，每个月可获得最大利润？最大利润是多少元？

解：（1）因为每件商品的售价上涨x元（x为整数），则商品的售价是________，每个月可售出____________件，由题意得y与x的函数关系式是____________________，自变量x的取值范围是____________________；

（2）结合（1）的函数关系知y=2200，得方程____________________，解方程得x=____________________，所以每件商品的售价应定为____________元；

（3）因为y与x的函数关系式是________________，因为a=________＜0，所以当x=________时，ymax=________元.故每件商品的售价应定为________元时，每个月可获得最大利润，最大利润是________元.

一、填空题

1.函数y=x2+2x-3的顶点坐标为__________，对称轴为__________，开口向__________，当________时，y随x的增大而__________；当________时，y随x的增大而__________，与x轴的交点坐标为__________.(www.xing528.com)

2.抛物线的开口向________，对称轴________，顶点坐标________.

3.要使函数y=（3a+2）x2+bx+c是二次函数，需要满足的条件是________________.

4.比较抛物线y=2x2与y=-2x2，它们的不同之处是________________.

5.函数y=kx+b的图像过点（2，1），（-1，4），则这个函数的解析式为________________.

6.抛物线y=x2-3x+2的对称轴为________________.

7.抛物线y=x2+4x+1与x轴有____________个交点.

8.二次函数y=x2+2x-5的最小值为________________.

9.若函数y=x2+4x+k的最小值等于3，则k的值等于________________.

10.直线y=2x-1与抛物线y=x2的公共点坐标是________________.

二、选择题

1.下列抛物线，对称轴是x=的是（　）.

A.y=　B.y=x2+2x

C.y=x2+x+2　D.y=x2-x-2

2.抛物线y=x2+6x+8与y轴的公共点坐标是（　）.

A.（0，8）　B.（0，-8）

C.（0，6）　D.（-2，0），（-4，0）

3.二次函数y=x2-2x+4的顶点坐标、对称轴分别是（　）.

A.（1，3），x=1　B.（-1，3），x=1

C.（-1，3），x=-1　D.（1，3），x=-1

4.用配方法将函数y=x2-4x+5写成y=a（x-h）2+k的形式为（　）.

A.y=（x+2）2+1　B.y=（x-2）2+1

C.y=（x+2）2-1　D.y=（x-2）2-1

5.已知函数f（x）=ax2+bx+c（a≠0）的大致图像如右图所示，则a，b，c的

符号为（　）.

A.a＞0，b＞0，c＞0　B.a＜0，b＜0，c＞0

C.a＞0，b＜0，c＜0　D.a＞0，b＞0，c＜0

一、填空题

1.二次函数的图像过点（1，-1），且开口向下的偶函数的解析式为________________，其增区间为____________.

2.如果函数y=x2+mx+2在区间（-∞，-2）上是减函数，在区间（-2，+∞）上是增函数，则m=________.

3.二次函数y=x2+mx+（m+3）与x轴有两个不同的交点，则m的取值范围是_________________.

4.抛物线y=x2-3x+2不经过第_________________象限.

5.设计周长为20 cm的矩形花台，则最大面积为_________________cm2.

二、选择题

1.已知二次函数y=kx2-7x-7的图像和x轴有公共点，则k的取值范围是（　）.

A.k＞　B.k≥且k≠0

C.k≥　D.k＞且k≠0

2.已知函数y=ax+b的图像经过第一、二、三象限，那么y=ax2+bx+1的图像大致为（　）.

A.

B.

C.

D.

3.函数y=x2+bx+c的图像经过点（-2，0），且关于直线x=1对称，则（　）.

A.b=-2，c=-8　B.b=-1，c=-6

C.b=1，c=-2　D.b=2，c=0

4.二次函数y=ax2+bx+c的图像如右图所示，则下列结论正确的是（　）.

A.a＞0，b＞0，c＜0　B.a＜0，b＜0，c＞0

C.a＜0，b＞0，c＜0　D.a＜0，b＞0，c＞0

三、解答题

1.已知二次函数图像的顶点是（-1，2），且过点，求二次函数的表达式，并画出其图像.

2.已知二次函数图像的顶点为（0，4），与x轴两交点间的距离为6，求：（1）图像与x轴两交点坐标；（2）二次函数的解析式；（3）解f（x）≥3.

3.已知矩形的周长为6，设矩形一边为x，它的面积为y，求：（1）y与x间的函数解析式，并写出自变量x的取值范围；（2）当x为何值时，矩形的面积最大？

4.某地区有一种可食用的野生菌，上市时，某商家按市场价格30元/kg收购了这种野生菌1000 kg存放入冷库中，据预测，该野生菌的市场价格每天上涨0.5元/kg；但冷冻存放这批野生菌时每天需要支出各种费用合计230元，而且这类野生菌在冷库中最多保存160天，同时，平均每天有3 kg的野生菌损坏不能出售.

（1）设x天后每千克该野生菌的市场价格为y元，写出y与x之间的函数关系式，并写出x的取值范围；

（2）若存放x天后，将这批野生菌一次性出售，设这批野生菌的销售总额为P元，写出P与x之间的函数关系式；

（3）该商家将这批野生菌存放多少天后出售可获得最大利润W元？（利润=销售总额-收购成本-各种费用）

5.已知二次函数y=-x2+2（m-1）x+2m-m2，（1）如果函数图像经过原点，求m的值；（2）如果函数图像关于y轴对称，写出函数关系式.

1.某学校先准备了可以建长24 m的墙的建筑材料，想利用一面墙设计修建如图所示的两矩形花台ABEF，FECD（其中墙EF共用）.设矩形ABCD的宽AB为x m，面积为S m2.

（1）写出S与x的函数关系式及x的取值范围；

（2）若矩形ABCD的面积为45 m2，求AB的长度；

（3）能修建比面积为45 m2更大的矩形花台吗？如果能，求出此最大面积；如果不能，请说明理由.

2.（2014年高考题）某人欲在墙角用长为3 m的铁丝网围一梯形状简易犬舍，如右图所示，设在梯形ABCD中，∠ABC=120°，∠BAD=90°，记BC=x，求：

（1）围成的犬舍面积S与x的函数关系式；

（2）当x取何值时，犬舍的面积最大，并求其最大值.

3.（2013年高考题）某经营企业生产A，B两种产品，根据市场调查和预测，对A产品投资1万才产生利润，并且利润是投资的一次函数，其关系如图1；B产品的利润是投资的算术平方根的正比例函数，其关系如图2.（注：利润与投资的单位为万元）

（1）分别写出A，B两种产品利润与投资的函数关系式；

（2）该企业已筹集到10万元资金，并全部投入A，B两种产品的生产，问：怎样分配这10万元投资，才能使企业获得最大利润，其最大利润为多少万元？

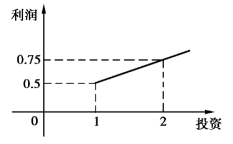
图1　

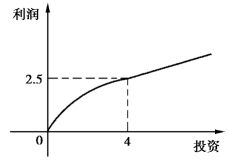
图2

自我评价

（满分100分，时间45分钟）　评价结果：__________

一、填空题（每题5分，共50分）

1.函数f（x）=x2-2x-1的最小值是________________.

2.二次函数f（x）=-x2+6x+3的顶点坐标为_____________，对称轴为______________.

3.二次函数f（x）=x2-3x-4与x轴的交点坐标是________________，与y轴的交点坐标是________________.

4.二次函数f（x）=x2-mx+3的对称轴为直线x=3，则m=________________.

5.抛物线f（x）=-3x2-x+4与x轴的交点个数是_________________.

6.已知函数y=（m-1）xm2+1+3x，当m=____________时，它是二次函数.

7.二次函数y=2x2-4x-3，当x=____________时，函数y有最________值是________.

8.用一根80 cm的铁丝，把它弯成一个矩形框，矩形框的最大面积是____________.

9.已知二次函数y=x2-6x+m的最小值是1，那么m的值是_____________.

10.已知二次函数的图像开口向下，且f（3）=5，对称轴为x=-1，则当f（x）≤5时，x的取值范围为________________.

二、选择题（每题5分，共20分）

1.二次函数y=x2+x-2的图像与x轴交点的横坐标是（　）.

A.2和-1　B.-2和1　C.2和1　D.-2和-1

2.二次函数y=x2-4x+3的图像交x轴于A，B两点，交y轴于C点，则△ABC的面积为（　）.

A.6　B.4　C.3　D.1

3.二次函数y=x2-2x-1的顶点式为（　）.

A.y=（x-1）2B.y=（x-1）2-2

C.y=（x+1）2+1　D.y=（x+1）2-2

4.二次函数y=x2+bx+c的图像上有两点（3，-8）和（-5，-8），则此拋物线的对称轴是（　）.

A.x=-1　B.x=1　C.x=2　D.x=3

三、解答题（每题10分，共30分）

1.已知一次函数y=f（x）且f（2）=5，f（3）=10，求f（4）.

2.当二次函数图像与x轴交点的横坐标分别是x1=-3，x2=1时，且与y轴交点为（0，-2），求这个二次函数的解析式.

3.（2015年高考题）某公司生产某种设备每年需固定支出120万元，此外每台设备还需支出其他费用2万元，设该公司年产量为x台，当x≤20时，公司年销售总收入为34x-x2万元；当x＞20时，公司年销售总收入为260+x万元.求：

（1）该公司年利润y与年产量x的函数关系式（年利润=年销售总收入-年总支出）；

（2）当该公司年产量为多少台时，所获年利润最大？最大利润是多少？

指数与对数

考纲内容：幂函数、指数函数和对数函数.

考纲要求：掌握指数与对数的概念、运算法则；了解幂函数、指数函数和对数函数的概念、图像和性质；能用函数、方程、不等式等知识解决有关简单实际问题.