函数的概念-中职数学升学考试教程

考点剖析：理解函数的定义、函数的3种表示方法；掌握简单函数定义域的求法.

1.函数的定义

设在某一变化过程中有两个变量x与y，如果按某个确定的对应关系f，使对于某个范围的任意一个数x，都有唯一的数y和它对应，那么就称y为x的函数，记作y=f（x），其中，x称为自变量，y称为因变量（或函数值），x的取值范围称为函数的定义域，y的取值范围称为函数的值域.

函数的三要素：定义域、对应关系、值域.

2.函数的3种表示方法

（1）列表法：用表格来表示函数的方法.

（2）公式法：用一个或几个等式来表示函数的方法.

（3）图像法：用平面直角坐标系里的图形来表示函数的方法.

3.求函数定义域的情形与方法

（1）分式的分母不等于0；

（2）偶次根式中，被开方式大于或等于0；

（3）函数y=x0中，底数不为0，即x≠0（00无意义）；

（4）对数中，对数的真数大于0；

（5）若y=tan x，则

【锦囊妙计】①求函数定义域，通常是根据以上情形列出不等式或不等式组求解集；

②在实际问题中，还要考虑自变量的实际意义.

【题型1】函数的定义

例　（1）若函数f（x）=-x+3，则f（-1）=________；若函数f（x）=5，则f（1）=________，f（x2）=________.

（2）若函数f（x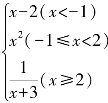）=，则f（4）=________，f（0）=________，f（-7）=________.

（3）若f（x）=x2+3x，则f［f（-1）］=____________，f（x-1）=____________.

（4）已知函数f（x）=2x+b，且f（1）=5，则b=________.

解：（1）4，5，5；（2），0，-9；（3）-2，x2+x-2；（4）3.

赢在起点

1.若函数f（x）=xa（其中a≠0），则f（1）=__________.

2.若函数f（x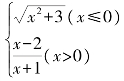）=，则f［f（-1）］=__________.

3.若函数f（x）=x2-2x+3，则f（x+1）=__________.

4.若函数f（x）=+m，且f（-1）=0，则f（1）=__________.

【题型2】求简单函数的定义域

例　求下列函数的定义域

（1）f（x）=（2）f（x）=

（3）f（x）=（4）f（x）=log2（x2-2x-3）

（5）f（x）=（6）f（x）=xa（a为负整数）

解：（1）要使f（x）有意义，必须满足x-3≠0⇔x≠3，

所以原函数的定义域是

（2）要使f（x）有意义，必须满足x2-3x-4≥0，

（x-4）（x+1）≥0，

x≤-1或x≥4，

所以原函数的定义域是x≤-1或x≥4｝.

（3）要使f（x）有意义，必须满足

所以原函数的定义域是≥-3且x≠-1｝.

（4）要使f（x）有意义，必须满足x2-2x-3＞0，

（x-3）（x+1）＞0，

x＜-1或x＞3，

所以原函数的定义域是或x＞3｝.

（5）要使f（x）有意义，必须满足

所以原函数的定义域是

（6）要使f（x）有意义，必须满足x≠0，

所以原函数的定义域是

赢在起点

求下列函数的定义域

（1）f（x）=，　（2）f（x）=，　（3）f（x）=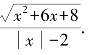

【题型3】判断相同的函数

例　下列各组函数中，表示相同函数的是（　）.

A.f（x）=与f（x）=2　B.f（x）=与f（x）=x

C.f（x）=与f（x）=　D.f（x）=2与f（x）=2x(www.xing528.com)

解：　C.

赢在起点

若函数与g（x）=+b表示同一函数，则a=________，b=________.

一、填空题

1.已知函数f（x）=x+1，则f（1）=________，f（x+2）=____________.

2.已知函数f（x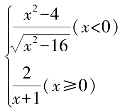）=，则f［f（-5）］=________________.

3.已知函数f（x）=x2+mx+n，且f（1）=1，f（-1）=2，则f（2）=____________.

4.函数f（x）=的定义域是____________.

5.函数f（x）=的定义域是____________.

6.函数f（x）=的定义域是________________.

7.函数f（x）=的定义域是________________.

8.函数f（x）=log2（x2-4）的定义域是________________.

9.函数f（x）=的定义域是________________.

10.函数f（x）=xa（a为正整数）的定义域是________________.

二、选择题

1.函数f（x）=的定义域是（　）.

A.或x≥5｝　B.≤x≤5｝

C.或x＞5｝　D.＜x＜5｝

2.函数f（x）=的定义域是（　）.

A.　B.且x≠2｝

C.　D.

3.函数f（x）=的定义域是（　）.

A.　B.

C.　D.

4.已知函数f（x）=log2（x2+3x+2），则其定义域是（　）.

A.（-2，-1）　B.［-2，-1］

C.（-∞，-2）∪（-1，+∞）　D.∅

一、填空题

1.已知函数f（x）=x2+3x+1，则f（x+1）=________________.

2.已知函数f（x）=ax3+bx+2，f（2）=8，则f（-2）=________________.

3.已知函数解析式为f（x）=6，则f（-3）=________，f（5）=________.

4.已知函数f（x）=x4+kx3+1，且f（-1）=6，则f（1）=________.

5.已知f（x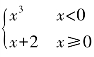）=，则f（-1）+f（3）=____________.

6.函数f（x）=的定义域是________________.

7.函数f（x）=的定义域是________________.

8.函数f（x）=的定义域是________________.

9.函数f（x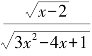）=的定义域是________________.

10.函数f（x）=的定义域是________________.

11.函数f（x）=的定义域是_________________.

二、选择题

1.函数f（x）=的定义域是（　）.

A.（1，2）　B.［1，2］

C.(-∞，1)∪（2，+∞）　D.∅

2.函数f（x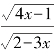）=的定义域是（　）.

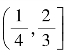A.　B.　C.　D.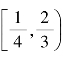

3.（2013年高考题）函数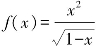+lg（3x+1）的定义域是（　）.

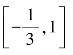A.　B.　C.　D.

三、解答题

1.已知函数g（x）=x2+px+q，满足g（1）=g（2）=0，求：（1）g（x）的解析式；（2）g（-1）.

2.已知函数f（x）=ax3+bx+c，且f（1）=5，f（2）=12，f（-1）=9，求f（-2）.

3.已知函数f（x+3）=2x+3，求函数f（x）的解析式.

1.已知f（x-1）的定义域为［1，3］，求函数f（x）的定义域.

2.若函数f（x）为二次函数，且f（0）=3，f（x+1）-f（x）=4x+2，求f（x）的解析式.