中职数学升学考试教程：含绝对值不等式

考点剖析：了解绝对值的几何意义和性质，掌握一元一次绝对值不等式的解法；能用集合、区间、数轴上的点集来表示其解集.

1.绝对值的几何意义：数轴上某个数到原点的距离称为它的绝对值.

2.绝对值的性质：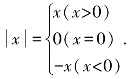

3.设0＜b＜a，则

（1）＞a⇔x＜-a或x＞a，

（2）＜a⇔-a＜x＜a，

（3）＞a⇔mx+n＜-a或mx+n＞a，

（4）＜a⇔-a＜mx+n＜a，

（5）

b＜＜a⇔-a＜mx+n＜-b或b＜mx+n＜a.

【锦囊妙计】解含有绝对值的不等式的关键是将其转化为一元一次不等式或不等式组，再解之.

【题型1】形如＜a（a＞0）类

例1　解不等式＜3.

解：原不等式为-3＜2x-1＜3⇔-2＜2x＜4

⇔-1＜x＜2

所以不等式的解集为

例2　解不等式

解：原不等式为＜5⇔-5＜3-2x＜5

⇔-8＜-2x＜2

⇔-1＜x＜4

所以不等式的解集为

例3　解不等式

解：原不等式为

⇔-2＜x-2＜2

⇔0＜x＜4

所以不等式的解集为

赢在起点

1.不等式＜1的解集是________________.

2.不等式＜10的解集是_________________.

3.不等式≥0的解集是________________.

【题型2】形如＞a（a＞0）类

例1　解不等式＞1.

解：原不等式为2x-1＜-1或2x-1＞1

解得x＜0或x＞1

所以不等式的解集为或x＞1｝.

例2　解不等式

解：原不等式为＞4⇔x-1＜-4或x-1＞4

⇔x＜-3或x＞5

所以不等式的解集为或x＞5｝.

例3　解不等式

解：原不等式为＞3⇔3x-2＜-3或3x-2＞3

⇔3x＜-1或3x＞5

⇔x＜或x＞

所以不等式的解集为或

赢在起点

1.不等式＞3的解集是_________________.

2.不等式＞12的解集是________________.

3.不等式-6＞0的解集是_________________.

【题型3】绝对值不等式的简单应用

例1　解不等式组.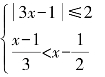

解：由≤2得-2≤3x-1≤2

所以-1≤3x≤3，即≤x≤1

又由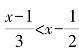得2（x-1）＜6x-3

所以

故不等式组的解集为

例2　解不等式1≤≤2.

解法1：原不等式为

⇔

所以不等式的解集为｛x-1≤x≤0或2≤x≤3｝.

解法2：-2≤x-1≤-1或1≤x-1≤2

所以不等式的解集为≤x≤0或2≤x≤3｝.

例3　已知集合，且A∪B=R，求a的取值范围.(www.xing528.com)

解：解得或x＞5｝

因A∪B=R，故集合A必须填满集合B在数轴上的空白（如右图所示）

可知a应满足不等式组

即1＜a＜3，所以a的取值范围为｛a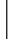1＜a＜3｝.

赢在起点

1.不等式组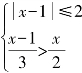的解集是________________.

2.不等式1≤≤5的解集是_________________.

一、填空题

1.不等式＞2的解集是________________；

2.不等式3＞15的解集是________________；

3.不等式-7≥0的解集是________________（用区间表示）；

4.不等式6-2≥0的解集是________________；

5.不等式≤7的解集是________________；

6.不等式≤3的解集是________________；

7.不等式2＜10的解集是________________（用区间表示）；

8.不等式10-2≥0的解集是________________；

9.不等式≤3的整数解是________________；

10.不等式≤1的正整数解是________________.

二、选择题

1.在数轴上与原点距离不大于2的点的坐标的集合是（　）.

A.或x≤-2｝　B.

C.　D.

2.不等式＞5的解集是（　）.

A.　B.

C.　D.或x＞7｝

3.＜2的整数解的个数有（　）.

A.0　B.1　C.2　D.3

4.不等式≥1的解集是（　）.

A.[1，+∞)　B.

C.　D.

5.不等式＜1的解集是（　）.

A.　B.

C.　D.或

一、填空题

1.不等式-3＞5的解集是________________.

2.不等式2+≤5的解集是________________（用区间表示）.

3.当a＞0，关于x的不等式＜a的解集是________________.

4.对于任意实数x，不等式≥m-1恒成立，则m的取值范围是________________.

5.设不等式＜b的解集为，则a=________，b=________.

6.不等式＜7的整数解为________________.

二、选择题

1.数轴上有一点M对应实数2，N点对应实数x，若M，N两点间的距离小于3，则x的取值范围是（　）.

A.[-1，5]　B.(-3，5)　C.(-1，5)　D.(-3，3)

2.不等式1≤＜2的解集是（　）.

A.　B.

C.　D.(-∞，0]∪[1，+∞)

3.已知a＞0，b＜0，a+b＜0，那么下列关系正确的是（　）.

A.-b＜-a＜0＜a＜b　B.b＜-a＜0＜a＜-b

C.-b＜-a＜0＜b＜a　D.b＜-a＜0＜-b＜a

4.若a＜-b＜0，则=（　）.

A.-2a　B.2a　C.-2b　D.2b

5.若a＞且b＜0，则（　）.

A.a+b＞0　B.a+b＜0　C.　D.b-a＞0

三、解答题

1.求不等式≤5的整数解.

2.（2013年高考题）解不等式组.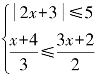

3.（2014年高考题）解不等式组.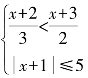

4.（2015年高考题）解不等式组.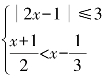

1.解不等式2＜≤7.

2.已知不等式＜a（a＞0）的解集是，试求a+2b的值.