中职数学升学考试教程：解一元二次不等式

考点剖析：掌握一元二次不等式的解法，能正确求出一元二次不等式的解集，能用集合、区间、数轴上的点集来表示其解集.

一元二次方程的根、根的判别式Δ、一元二次函数、一元二次不等式的解集的关系如下表：

1.当a＞0时

【锦囊妙计】当a＞0，一元二次方程有两个不同实数根时可借助口诀“小于夹中间，大于找两边”求一元二次不等式的解集.

2.当a＜0时

【题型1】能因式分解的一元二次不等式

例1　解不等式x2-2x-3＞0.

解：原不等式为（x-3）（x+1）＞0

⇔x＞3或x＜-1

所以不等式的解集为或x＜-1｝.

例2　解不等式-x2-3x+4≥0.

解：不等式为x2+3x-4≤0

⇔（x+4）（x-1）≤0

⇔-4≤x≤1

所以不等式的解集为

例3　解不等式x2-2x+1＞0.

解：不等式为（x-1）2＞0

（x-1）2=0有两个相等实数根x1=x2=1

x2-2x+1＞0⇔x≠1

所以不等式的解集为

赢在起点

1.一元二次不等式（x+2）（x-5）＜0的解集是________________.

2.一元二次不等式x2-x-12＞0的解集是________________.

3.一元二次不等式x2-6x+9＞0的解集是______________.

【题型2】不能因式分解的一元二次不等式

例1　解不等式x2-x-1＞0.

解：x2-x-1=0的判别式Δ=（-1）2-4×1×（-1）=5＞0

x1、2=

x2-x-1＞0⇔x＜或

所以不等式的解集为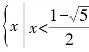或

例2　解不等式x2-2x+4＞0.

解：x2-2x+4=0的判别式Δ=（-2）2-4×1×4=-12＜0，

因此方程没有实数根，

从而函数y=x2-2x+4的图像与x轴没有交点，草图如右图所示：

x2-2x+4＞0⇔x∈(-∞，+∞)

所以不等式的解集为R.

例3　解不等式2x2-x+1＜0.

解：2x2-x+1=0的判别式Δ=（-1）2-4×2×1=-7＜0

因此方程没有实数根，

从而函数y=2x2-x+1的图像与x轴没有交点，草图如例2的图所示，

对于一切实数x都有2x2-x+1＞0，

所以2x2-x+1＜0的解集为∅.

赢在起点

1.一元二次不等式x2-2x-1＜0的解集是________________.

2.一元二次不等式x2-x-1＞0的解集是________________.

3.一元二次不等式x2-x-1＜0的解集是__________________.

【题型3】一元二次不等式的应用

例1　如下图，已知不等式ax2-2x+a＞0的解集为R，求实数a的取值范围.

解：若满足题意条件，则有

解得或

所以a的取值范围是.

例2　已知不等式2x2+mx+n＞0的解集是或x＜-2｝，试求：（1）m，n的值；（2）不等式2x2-mx+n≤0的解集.

解：（1）由一元二次方程的根和一元二次不等式的解集的关系知：-2和3是方程2x2+mx+n=0的两根，由韦达定理可得-2+3=

所以m=-2，n=-12

（2）不等式2x2-mx+n≤0为2x2+2x-12≤0化简得

x2+x-6≤0

所以它的解集为

例3　某商店将一种进货单价40元的商品按50元一个出售时一周能卖出300个，若每涨价1元，其销售量就减少10个，问如果商店每周销售该商品的利润不小于3750元，则销售单价应为多少？

解：设商品单价涨价x次1元，由题意得

（50-40+x）（300-10x）≥3750（0≤x≤30，且x∈N）

3 000-100x+300x-10x2≥3750

化简得-10x2+200x-750≥0⇔x2-20x+75≤0

⇔（x-5）（x-15）≤0(www.xing528.com)

⇔5≤x≤15

答：该商品的销售单价应在55元到65元间时，每周利润不小于3750元.

赢在起点

1.如果不等式x2+bx+＞0的解集为R，那么实数b的取值范围是____________.

2.如果不等式ax2-2x+a＞0的解集为∅，那么实数a的取值范围是____________.

3.如果不等式x2+mx+n＜0的解集是，m=__________，n=______________.

一、填空题

1.不等式（x+1）（x-2）＜0的解集是________________（用区间表示）.

2.不等式（x+2）（x-3）＞0的解集是_________________（用区间表示）.

3.不等式3x2-2x≤0的解集是________________.

4.不等式x2+5x+6＜0的解集是_________________.

5.不等式x2-7x+6≥0的解集是________________.

6.不等式x2≤16的解集是________________.

7.不等式x2-x-12＜0的解集是________________.

8.不等式x2-2x≥3的解集是________________（用区间表示）.

9.不等式x2+12＜7x的解集是________________.

10.不等式x2+5＜0的解集是________________.

二、选择题

1.不等式x2-x-2＜0的解集是（　）.

A.（-2，1）　B.（-∞，-2）∪（1，+∞）

C.（-1，2）　D.（-∞，-1）∪（2，+∞）

2.不等式4x-x2＜-5的解集是（　）.

A.(-1，5)　B.(-∞，-1)∪(5，+∞)

C.(-5，1)　D.(-∞，-5)∪(1，+∞)

3.不等式（x-2）2≤4的解集是（　）.

A.　B.或x≥2｝

C.≤x≤4｝　D.或x≥4｝

4.已知不等式ax2+bx+c＜0（a≠0）的解集是R，则（　）.

A.a＞0，Δ＜0　B.a＞0，Δ＞0

C.a＜0，Δ＜0　D.a＜0，Δ＞0

5.若a＞b＞0，则不等式x2-（a+b）x+ab＜0的解集是（　）.

A.或x＜b｝　B.或x＞b｝

C.　D.

一、填空题

1.不等式（x-1）（1-2x）＞0的解集是________________.

2.不等式（2x-1）2≤9的解集是________________（用区间表示）.

3.已知集合，则集合M∩N=_________________.

4.已知不等式x2+px+q＜0的解集是，则p+q=________________.

5.已知方程x2+（m-3）x+m=0有实根，则m的取值范围是________________.

6.已知（ax-1）（x-1）＞0的解集是，则实数a的值为______________.

二、选择题

1.若一元二次方程x2-mx+1=0有两个不等的实数根，则下列各式中成立的是（　）.

A.m＞2　B.-2＜m＜2

C.m＜-2　D.m＜-2或m＞2

2.函数的定义域是（　）.

A.R　B.［-3，3］

C.(-∞，-3)∪(3，+∞)　D.(-∞，-3]∪[3，+∞)

3.不等式（x-1）（2-x）≥0的解集是（　）.

A.或x≤2｝　B.

C.或x≤-2｝　D.

4.若恒成立，则m的取值范围是（　）.

A.或m＜0｝　B.

C.或m＜0｝　D.

5.不等式x2+mx+1＜0的解集是∅，则m的取值范围是（　）.

A.R　B.（-2，2）

C.（-∞，-2）∪（2，+∞）　D.［-2，2］

1.已知不等式mx2+mx+2＜0的解集为∅，求实数m的取值范围.

2.关于x不等式（a-2）x2+2（a-2）x-4＜0的解集为R，求实数a的取值范围.

3.已知不等式x2+mx+n＞0的解集是或x＞2｝，试求：

（1）m，n的值；（2）不等式x2-mx+n＜0的解集.

4.某公司欲将一批新鲜蔬菜用汽车从甲地运往125 km以外的乙地，运费为每小时30元，装卸费为1000元，蔬菜在运输途中的损耗费（单位：元）是汽车速度（km／h）值的2倍，为使运输的总费用（包括运费、装卸费和损耗费）不超过1200元，汽车的最高速度应为每小时多少公里？