一元一次不等式及性质简介

考点剖析：理解不等式的基本性质；能运用性质判断命题的正误；了解用作差法比较大小；了解不等式的证明；掌握一元一次不等式（组）的解法，并能用集合、区间、数轴上的点集来表示其解集.

1.对a，b∈R，均有：a-b＞0⇔a＞b，

a-b=0⇔a=b，

a-b＜0⇔a＜b.

2.不等式的重要性质

（1）对称性：a＞b⇔b＜a.

（2）传递性：a＞b，b＞c⇒a＞c（或a＜b，b＜c⇒a＜c）.

（3）基本性质：①a＞b⇒a+c＞b+c；

②a＞b，c＞0⇒ac＞bc；

a＞b，c＜0⇒ac＜bc.

（4）移项法则：a+b＞c⇒a＞c-b.

（5）同向不等式的可加性：

（6）同向正数不等式的可乘性：

3.不等式的证明方法有：差值比较法、综合法等.

4.用区间表示集合：设b＜a，则

｛xb≤x≤a ｝=[b，a]，｛xb≤x＜a ｝=[b，a)，｛xb＜x≤a｝=(b，a]，

｛xb＜x＜a｝=（b，a），｛xx＞a ｝=（a，+∞），｛xx＜a｝=（-∞，a）.

5.一元一次不等式组的解集的4种情况：设b＜a，则

（1）即（a，+∞），（2）即（-∞，b），

（3）即（b，a），（4）

【锦囊妙计】一元一次不等式组的解集可以用口诀帮助记忆：“同大取大，同小取小，大小小大中间找，大大小小找不了”.

【题型1】不等式的基本性质

例　选择题

（1）设a，b，c，d∈R，且a＞b，c＞d，则下列结论中正确的是（　）.

A.a+c＞b+d　B.a-c＞b-d　C.ac＞bd　D.

（2）设a，b，c∈R，且a＜b，则下列不等式中一定成立的是（　）.

A.c-a＜c-b　B.c+a＜c+b　C.ac＜bc　D.

（3）若a，b为任意实数，且a＞b，则（　）.

A.a2＞b2　B.　C.lg（a-b）＞0　D.

（4）若，则下列不等式：①a+b＜ab，②，③a＜b，④a2-ab＜0，成立的式子有（　）.

A.1个　B.2个　C.3个　D.4个

解：（1）A；（2）B；（3）D；（4）B

【锦囊妙计】在做选择题（4）时可以用符合条件的特殊值代入结论判断结论是否成立.

赢在起点

1.若a＜b，c＜d，则a+c________b+d（填＞或＜）.

2.若a＜b＜0，c＜d＜0，则ac________bc（填＞或＜）.

3.若x＜0，y＞0，则x-y________0（填＞或＜）.

【题型2】解不等式（组）

例1　填空题

（1）不等式的解集为_________________.

（2）不等式组的解集为________________（用区间表示）.

（3）不等式组的解集为________________.

解：（1）；（2）（3，+∞）；（3）

例2　解不等式组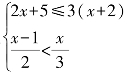

解：由2x+5≤3（x+2）得x≥-1，

又由得3（x-1）＜2x，解得x＜3，

所以不等式组的解集是

赢在起点

1.不等式的解集为________________.

2.不等式组的解集为________________（用区间表示）.

3.不等式组的解集为________________.

【题型3】比较两个代数式的大小

例1　若x＞2，比较x3与2x2-2x+4的大小.

解：x3-（2x2-2x+4）=x3-2x2+2x-4=（x3+2x）-（2x2+4）

=x（x2+2）-2（x2+2）=（x2+2）（x-2）

因为x＞2，所以x-2＞0且x2+2＞0

得（x2+2）（x-2）＞0

所以x3＞2x2-2x+4.

例2　比较a2+b2+5与2（2a-b）的大小.

解：因为a2+b2+5-2（2a-b）=a2+b2+5-4a+2b　

=（a2-4a+22-22）+（b2+2b+12-12）+5　

=（a-2）2+（b+1）2≥0

所以a2+b2+5≥2（2a-b）.

赢在起点

1.若x≠y，则x2+y2______________2xy（填＞或＜）.

2.比较（x+2）（x+3）________（x-2）（x+7）（填＞或＜）.

【题型4】证明不等式

例1　求证：当a＞b时，a3-b3＞ab（a-b）

证明：a3-b3-ab（a-b）=a3-b3-a2b+ab2

=（a3-a2b）-（b3-ab2）

=a2（a-b）-b2（a-b）

=（a-b）（a2+b2）

因为a＞b，所以a-b＞0，a2+b2＞0即（a-b）（a2+b2）＞0

所以a3-b3＞ab（a-b）.

例2　求证：当x，y∈R时，x（2x-1）＞x2+x-2

证明：x（2x-1）-（x2+x-2）=2x2-x-x2-x+2(www.xing528.com)

=x2-2x+2

=（x-1）2+1

因为（x-1）2+1＞0，所以x（2x-1）＞x2+x-2.

赢在起点

1.求证：当a+b＞0，且a≠b时，a3+b3＞a2b+ab2

证明：a3+b3-（a2b+ab2）=________________________；

=________________________；

=________________________；

=________________________；

因为_________________________________________＞0，所以a3+b3＞a2b+ab2.

2.求证：当x，y∈R时，x（2x+1）＞x2-x-3

证明：x（2x+1）-（x2-x-3）=________________________；

=________________________；

=________________________；

因为________________________＞0，所以x（2x+1）＞x2-x-3.

【锦囊妙计】作差法比较大小或证明不等式的思路为：作差→变形→判号→结论，为便于判号，作差化简后通常用因式分解和配方两种方法变形.

一、填空题

1.设x-5＜2，则x＜________；设3x-1＞5，则x＞________；设1-2x＞7，则x＜________.

2.用“＞或＜”填空.

（1）如果a＞b，那么2a________a+b，a-3________b-5.

（2）如果a＜b＜0，则.

（3）如果-2x＞-2y，那么x________y.

（4）如果3-x＞2，那么x________1.

（5）如果a＜b＜0，那么ab________0.

3.一元一次不等式组的解集为________________.

4.一元一次不等式组的解集为________________.

5.一元一次不等式组的解集为________________.

6.一元一次不等式组的解集为________________.

7.一元一次不等式组的解集为________________.

8.一元一次不等式组的解集为________________（用区间表示）.

9.不等式1≤x≤2用区间表示为________________.

二、选择题

1.一元一次不等式3x+9＞0的解集是（　）.

A.　B.　C.　D.

2.若x＞y，则下列式子错误的是（　）.

A.x-2＞y-2　B.2-x＞2-y　C.x+3＞y+2　D.

3.（2013年高考题）命题“x＞0，y＞0”是命题“xy＞0”的（　）.

A.充分而不必要条件　B.必要而不充分条件

C.充要条件　D.既不充分也不必要条件

4.设a＜0，且，则下列命题正确的是（　）.

A.a+b＜0　B.b-a＞0　C.a-b＞0　D.

5.若，则下列命题正确的是（　）.

A.a＞0，b＜0　B.a＜0，b＞0

C.a＞0，b＞0或a＜0，b＜0　D.a＜0，b＞0或a＞0，b＜0

6.如果a，b，c，d是任意实数，则下列命题正确的是（　）.

A.若a＞b，c＞d，则a＞d　B.若a＞-b，则c+a＞c-b

C.若a＞b，则ac2＞bc2　D.若a＞b，c＜0，则ac＞bc

一、填空题

1.不等式-2x＞-10的解集为________________（用区间表示）.

2.不等式的解集是________________.

3.一元一次不等式组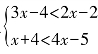的解集为________________.

4.一元一次不等式组的整数解有________________个.

5.一元一次不等式组的正整数解有________________个.

二、选择题

1.ab＞0是a＜0且b＜0的（　）.

A.充分而不必要条件　B.必要而不充分条件

C.充要条件　D.既不充分也不必要条件

2.若a＜b＜0，则下列不等式中错误的是（　）.

A.ab＞0　B.a-b＜0　C.a+b＜0　D.

3.下列命题中正确的是（　）.

A.若x2＞x，则x＞0　B.若x2＞0，则x＞0

C.若x＜0，则x2＞x　D.若x＜1，则x2＜x

4.若，则下列结论错误的是（　）.

A.a2＜b2B.a＜b　C.ab＜b2D.a2＜ab

5.已知a＞b，c＞d，则下列命题中正确的是（　）.

A.a-c＞b-d　B.　C.ac＞bd　D.c-b＞d-a

三、解答题

1.解不等式组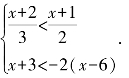

2.解不等式

3.解不等式组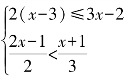（解集用区间表示）.

1.比较大小.

（1）（x+3）（x-4）与（x+2）（x-3）；（2）已知0＜a＜b，a3-b3与ab2-a2b；

（3）a2+b2与2a-4b-5.

2.已知a，b都是正数，且a≠b，求证a4+b4＞ab（a2+b2）.