集合运算：交集、并集、补集简析

考点剖析：理解和掌握交集、并集、补集的定义；了解全集的定义，能正确求两个集合的交集、并集以及集合的补集.

1.交集：由既属于集合A又属于集合B的元素组成的集合称为A与B的交集，记作A∩B（如右图阴影部分），即A∩B=｛xx∈A且x∈B｝.其主要性质有：

（1）A∩B=B∩A；　（2）A∩A=A；　（3）A∩∅=∅.

2.并集：由所有属于集合A或属于集合B的元素组成的集合称为A与B的并集，记作A∪B（如左图阴影部分），即A∪B=｛xx∈A 或x∈B｝，其主要性质有：

（1）A∪B=B∪A；　（2）A∪A=A；

（3）A∪∅=A.

注：若A⊆B，则A∩B=A，A∪B=B.

3.全集：一般地，如果一个集合含有我们研究问题中涉及的所有元素，那么就称这个集合为全集，通常记为U或I.

4.补集：设U是全集，且A⊆U，由U中所有不属于A的元素组成的集合，称为集合A在U中的补集（如右图阴影部分），记作CUA，即CUA=｛xx∈U，且x∉A｝，其主要性质有：

（1）A∩CUA=∅；　（2）A∪CUA=U；　（3）CU（CUA）=A.

【题型1】求交集

例1　（1）已知集合A=｛2，3，4｝，B=｛3，4，5｝，则M∩N=（　）.

A.｛0，2，5｝　B.｛3，4｝　C.｛2，5｝　D.｛2，3，4，5｝

（2）已知集合A=｛1，2，3，4｝，B=｛x x≤3，x∈N｝，求A∩B.

A.｛1，4｝　B.｛2，3｝　C.｛9，16｝　D.｛1，2，3｝

解：（1）B；（2）　D.

例2　已知集合A=｛x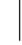3≤x＜7｝，B=｛x 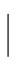2＜x＜10｝，求A∩B.

解：A∩B=｛x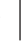3≤x＜7且2＜x＜10｝=｛x2＜x＜7｝.

赢在起点

1.若集合A=｛a，b，d｝，集合B=｛b，c，d，e｝，则A∩B=________________.

2.若集合，集合，则A∩B=________________.

3.若集合A=｛（x，y）｝，集合B=｛（x，y）｝，则A∩B=________________.

【题型2】求并集

例1　（1）设集合A=｛-1，2｝，B=｛-1，0，1｝，，则A∪B=（　）.

A.｛0｝　B.｛0，2｝　C.｛-1，0，1，2｝　D.｛0，1，2｝

（2）设集合A=｛x -5≤x＜1｝，B=｛xx≤2｝，则A∪B=（　）.

A.｛x-5≤x＜1｝　B.｛x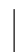-5≤x≤2｝　C.｛x 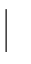x＜1｝　D.｛x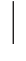x≤2｝

解：（1）C；（2）　D.

例2　已知集合A=｛x-1＜x＜2｝，B=｛x 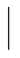1＜x＜3｝，求A∪B.

解：A∪B=｛x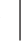-1＜x＜2或1＜x＜3｝=｛x-1＜x＜3｝.

赢在起点

1.已知集合A=｛4，5，6，8｝，B=｛3，5，7，8｝，则A∪B=_________________.

2.已知集合A=｛x-7＜x＜2｝，B=｛x-1＜x＜3｝，则A∪B=________________.

3.已知集合A=｛x-5＜x＜1｝，B=｛xx＞2｝，则A∪B=________________.

【题型3】求补集

例1　设全集U=｛0，1，2，3，4｝，A=｛1，3｝，则CUA=（　）.

A.∅　B.｛2，4｝　C.｛0，1，3｝　D.｛0，2，4｝

解：　D.

例2　已知全集U=R，集合A=｛xx+1＜0｝，求CUA.

解：CUA=｛x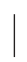x≥-1｝.

例3　已知全集U=｛x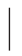x是小于9的正整数｝，集合A=｛1，2，3｝，求CUA.

解：根据题意可知，U=｛1，2，3，4，5，6，7，8｝，所以CUA=｛4，5，6，7，8｝.

赢在起点

1.设全集U=｛-1，2，3，4｝，A=｛2，3｝，则CUA=________.

2.已知全集U=R，集合A=｛x？x＜3｝，则CUA=____________.

【题型4】交集、并集、补集的综合应用

例1　设全集U=｛xx∈N*且x≤7｝，集合A=｛2，4，7｝，B=｛1，2，3｝，则A∩CUB=________；

解：A∩CUB=｛4，7｝.

例2　已知A={（x，y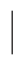）2x+3y=8}，B={（x，y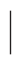）3x-2y=-1}，求A∩B.

解：由题意得，解之得，

所以A∩B=｛（1，2）｝.

特别强调：｛1，2｝、｛（1，2）｝、｛（2，1）｝是3个不同的集合，上述结果也可表示为A∩B=｛（x，y）x=1，y=2｝.

例3　设集合A=｛x2，2x-1，-4｝，B=｛x-5，1-x，9｝，若A∩B=｛9｝，求A∪B.

解：因为9∈A∩B，因此x2=9或2x-1=9，解得x=±3或x=5；

（1）当x=3时，A=｛9，5，-4｝，B=｛-2，-2，9｝，故x=3应舍去；

（2）当x=-3时，A=｛9，-7，-4｝，B=｛-8，4，9｝，A∩B=｛9｝满足题意，所以当x=-3，此时A∪B=｛-8，-7，-4，4，9｝；

（3）当x=5时，A=｛25，9，-4｝，B=｛0，-4，9｝，此时A∩B=｛-4，9｝，这与A∩B=｛9｝矛盾，故x=5应舍去.

综上得x=-3，且A∪B=｛-8，-7，-4，4，9｝.(www.xing528.com)

赢在起点

1.设集合A=｛x 2≤x＜4｝，B=｛x 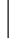3x-7≥8-2x｝，则A∪B=__________，A∩B=__________.　

2.已知A=｛（x，y）|x+3y=7｝，B=|｛（x，y）|x-y=-1｝，则A∩B=____________

一、填空题

1.设A=｛1，2｝，B=｛-1，0，1｝，则A∩B=________.

2.设集合A=｛a，b｝，B=｛b，c｝，则A∪B=________.

3.已知集合M=｛1，2，3，4｝，N=｛5，6｝，则M∩N=________，M∪N=________.

4.已知集合A=｛1，2，3，4，5｝，B=｛1，3，5，7｝，则A∩B=________.

5.已知集合M=｛a，b，c｝，N=｛b，c，d，f｝，则M∪N=________.

6.设集合A=｛自然数｝，B=｛x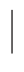-2016≤x＜3｝，则A∩B=________.

7.已知集合A=｛x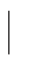-3≤x≤2｝，B=｛xx＞1｝，则A∩B=________，A∪B=________.

8.设集合A=｛（x，y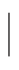）2x-y=3｝，B=｛（x，y）2x+y=5｝，则A∩B=____________.

二、选择题

1.（2013年高考题）已知集合A=｛0，1｝，B=｛1，2｝，则A∪B=（　）.

A.｛1｝　B.｛0，1｝　C.｛1，2｝　D.｛0，1，2｝

2.已知集合A=｛2，3｝，B=｛3，4｝，则A∩B=（　）.

A.｛2，3｝　B.｛3｝　C.｛3，4｝　D.｛2，3，4｝

3.已知集合A=｛a，b｝，B=｛b，c｝，则A∩B=（　）.

A.｛a，b｝　B.｛b，c｝　C.｛b｝　D.｛a，b，c｝

4.已知集合M=｛a，b｝，N=｛b，c，d｝，则M∪N=（　）.

A.｛b｝　B.｛a，c，d｝　C.｛a，b，c｝　D.｛a，b，c，d｝

5.已知集合M=｛2，3，4｝，N=｛2，4，6，8｝，则M∩N=（　）.

A.｛2｝　B.｛2，4｝　C.｛2，3，4，6，8｝　D.｛3，6，8｝

6.设集合，则M∩N=（　）.

A.R　B.∅　C.　D.

7.设集合，则A∪B=（　）.

A.　B.　C.　D.

一、填空题

1.已知全集U=｛a，b，c，d，e｝，集合A=｛a，b，d｝，B=｛a，c｝，那么CU（A∩B）=________.

2.已知集合，则A∩B=________，那么A∪B=________.

3.已知集合，那么A∩B=________.

4.已知全集U=｛-3，-2，-1，0，1，2｝，，x∈Z｝，则CUA=________.

5.设全集，且n＜5｝，A=｛1，3｝，B=｛2，4｝，则CU（A∪B）=________.

二、选择题

1.设全集U=｛a，b，c，d，e｝，集合A=｛a，b，d｝，B=｛b，d｝，则CUA∩CUB=（　）.

A.｛c，e｝　B.｛b，c，d｝　C.｛b，d｝　D.｛a，b，d，e｝

2.设全集U=｛0，1，2，3，4｝，集合A=｛0，1，2，3｝，B=｛2，3，4｝，则CUA∪CUB=（　）.

A.｛0｝　B.｛0，1｝　C.｛0，1，4｝　D.｛0，1，2，3，4｝

3.设全集U=｛不大于7的正整数｝，集合A=｛3，4，6｝，B=｛3，4，5｝，则CU（A∩B）=（　）.

A.｛0，1，2，5，6，7｝　B.｛1，2，5，6｝　C.｛0，1，2，5，6｝　D.｛1，2，5，6，7｝

4.（2013年高考题）已知集合A=｛0，1｝，B=｛1，2｝，则A∪B=（　）.

A.｛1｝　B.｛0，1｝　C.｛1，2｝　D.｛0，1，2｝

5.（2014年高考题）已知集合A=｛1，2，3｝，B=｛1，3，5｝，则A∩B=（　）.

A.｛1｝　B.｛1，3｝　C.｛2，5｝　D.｛1，2，3，5｝

6.（2015年高考题）已知全集U=｛1，2，3，4，5｝，A=｛1，3，5｝，则CUA=（　）.

A.∅　B.｛2，4｝　C.｛1，3，5｝　D.｛1，2，3，4，5｝

三、解答题

1.已知集合A=｛1，3，a｝，B=｛1，a2-a+1｝，且A∪B=A，求实数a的值.

2.已知a∈R，集合A=｛a-1，2a-1，a2+1｝，B=｛-3，a，2｝，如果A∩B=｛-3｝，求实数a的值.

3.若集合，求A∩B.

1.已知集合，设全集U=R，

求：（1）CUA；（2）CUB；（3）CUA∪CUB.

2.设全集，x∈Z｝，集合，集合，x∈N｝，

求：（1）CUB；（2）A∩B；（3）CUA∩B；（4）CU（A∪B）.

逻辑用语部分

考纲内容：充要条件.

考纲要求：掌握简单的充分条件、必要条件和充要条件的判定方法.