方格网法、断面法、等高线法，哪个更精确？

土方量的计算实质是体积的计算，其计算的宗旨公式是V=S×h。但实际工作中，土石方的计算又是一项很复杂而烦琐的工作，这主要是因为土方体积包含各种各样的情形，如坑塘洼地填土、道路建设开挖、土地填挖平整、山头爆破取石、海岸吹填沙，等等。针对不同的情形使用不同的计算方法如平均高程法、方格网法、断面法、等高线法等，可获得理想的计算效果与精度。

1.平均高程法

平均高程法是经常使用的一种土方量计算方法，在以前使用纸质地形图的年代尤其适用，其实质就是总面积S乘平均高差h，即

式中，V为填（或挖）总土方量；S为填（或挖）总面积；H平为平均高程；H设为设计高程。

上述平均高程H平为根据现状地形图计算出的加权平均高程。加权时主要根据高程点的面积控制范围进行加权。例如，计算图8-25所示范围内的高程平均值，则图中的各格网交叉点对高程的控制加权平均值可按下式计算：

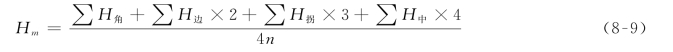
式中，n为测区范围内小方格网的个数；Hm为测区平均高程；H角为只涉及一个小方格的角点高程；H边为涉及两个小方格的边点高程；H拐为涉及三个小方格的拐点高程；H中为影响四个小方格的中点高程。如图8-25所示，有1、3、4、12、16、18六个角点，2、7、8、11、15、17六个边点，5、13两个拐点，6、9、10、14四个中点，共18个交叉点。

式（8-9）只是计算高程加权平均值的理论公式。工程实际中的边界不可能像图8-25所示那样方正，因此其高程的加权平均值计算就应根据实际情况考虑。现在的平均高程计算已普遍用计算机软件自动进行。

2.方格网法

前面介绍了用方格网计算面积的情形。与此相类似，土方体积计算也可按此法进行。这种方法一般适合于大范围的、填（挖）厚度比较均匀的情况，而在当今电子地形图盛行的年代更是大行其道。下面的例子适合于用纸质地形图或电子地形图进行土石方工程计算。

图8-26所示是一块地进行填、挖土地平整的地形图的局部，图中等高距为1 m，等高线高程分别有51 m、52 m、…、58 m。工作时先根据设计的平土高程H设绘出填、挖分界线（图中虚线，高程为H设=54.4 m），按一定边长（如可按图上1×1 cm2或2×2 cm2）绘纵、横方格线1、2、3、4、5、6及A、B、C、D，然后进行如下计算。

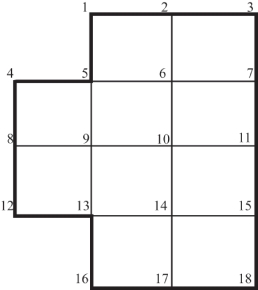
图8-25　高程点的权影响

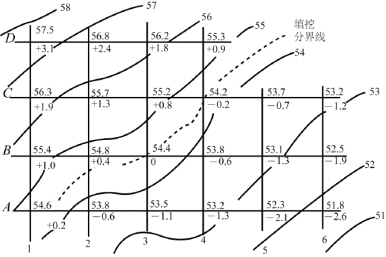
图8-26　用方格网计算土方量

①用内插法计算方格网交叉点的高程并标注在交叉点右上方，如图8-26所示。

②根据平土设计高程和各交叉点高程计算各点的填（挖）高差，标注于交叉点的右下方。“+”表示挖方，“-”表示填方。

③用上述的交叉点高差取平均值计算小方格的填（挖）高差hm。对于填（挖）分界线所在的方格，则需分开计算。(www.xing528.com)

④计算小方格的挖（填）方量体积V=S×hm，这里S为小方格的实地面积。对于填（挖）分界线所在的方格，同样需分开计算。

⑤累加各小方格的体积，得总的工程挖（填）方量。

3.等高线法

等高线法主要适合于整座山体自上而下的采挖过程，露天矿的往下开采也属于这种情况。图8-27所示是应用这种方法的典型案例图。

图中，规划将整个山头爆破平土至65 m等高线位置，要求预算工程量大小。

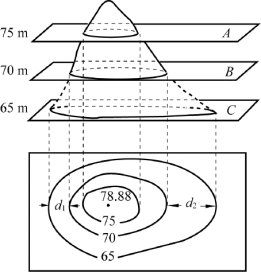
图8-27　等高线法计算土方量

实际中，可用求积仪量测出各条等高线所包含的面积，分别计算相邻等高线之间台柱体的体积，然后累加则得总土石方工程量。图8-27所示山体由三段台柱墩组成，即有

将h=5 m代入，同时将各条等高线围成的实地面积代入，便可计算得总工程方量。

4.断面法

图8-23介绍了断面图绘制的基本原理。根据此原理，我们可以在某些线路，例如铁路、公路、水渠等工程设计和方案规划预算中，采用该方法进行土石方工程计算。图8-28所示是用断面法计算体积的基本原理图。

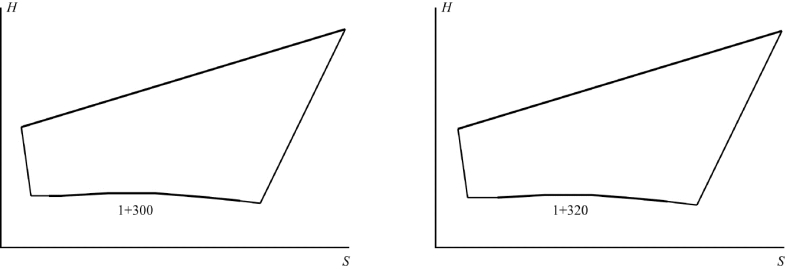
图8-28　断面法计算土方量

图8-28绘出了公路沿线某两条相邻里程桩1+300、1+320所在的横断面图，它们分别反映了各自在横断面方向的地表形态，同时也反映出各自在横断面位置需要开挖（或回填）至基本高程面的面积S1+300、S1+320。显然，只要求出这两个断面的面积，用它们的平均值与断面之间的距离相乘，便得到这两断面之间的体积。计算公式为

式中断面之间的距离L就是它们的里程桩桩号之差，图8-28中两断面相距L=20 m，这是公路设计中经常使用的20 m桩号之间的距离。