先考虑一个关于三角形外接圆的几何问题。
如图7-29所示，以AB为固定底边、顶角为α的三角形有无数个，这些三角形的顶点可以在△ABP的外接圆上随意滑动。另外，以BC为固定底边、顶角为β的三角形也有无数个，同样这些三角形的顶点也在△BCP的外接圆上滑动。当三角形的顶点都滑动到两外接圆相交处P点时，形成两个具有公共边PB的三角形。换句话说，只有在P点才能绘出顶角为α和β的两个三角形——△PAB和△PBC。这便是后方交会的几何基础。
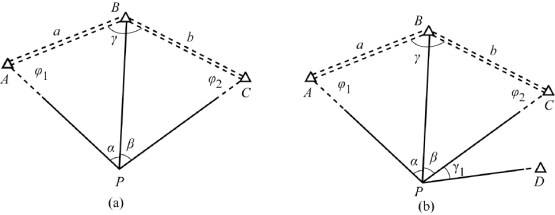
如图7-30（a）所示，仅在待定点P设站，向三个已知控制点观测两个水平夹角α、β，从而计算出待定点的坐标，这便是传统的测角后方交会。
由于图7-30（a）中也只有两个观测值，刚好只能计算出待定点P的坐标，没有检核条件，所以实际中还会瞄准第四个已知控制点D来测量一个多余观测值γ1，作为检核条件，如图7-30（b）所示。检核的方法与前述侧方交会情况相同。如检核合格，也可以从四个已知控制点中重新挑选出三个图形条件比较好的控制点，再计算出一套待定点坐标，与之前坐标对照取平均值。这里的图形条件比较好主要是指待定点能避开后方交会的危险圆范围。
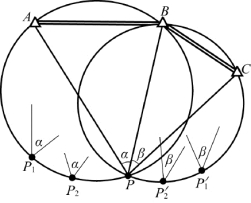
图7-29 后方交会的几何原理
(www.xing528.com)
图7-30 后方交会
后方交会的解算方法很多。由于全站仪的广泛使用，传统的测角后方交会已经很少采纳，因此这里不予阐述。有兴趣者可查阅参考文献［8］《基础测绘学》相关章节内容。
后方交会的最大好处是只需在待定点摆一个站观测，不必在已知控制点摆站，这大大提高了野外作业的工作效率，缺点是操作人员容易忽略危险圆对点位的影响，又因为时间紧张而匆忙收工，缺少多余观测从而给后面的工作带来烦恼。这里要提醒大家的是，在野外一定要多观测一个甚至两个已知方向，作为备用观测。
【名词解释——危险圆】 如图7-31所示，后方交会的三个目标控制点A、B、C确定了一个外接圆。显然，如果我们不小心在这个圆周上选取了待定点摆站观测，无论点位选在这个圆周的哪个位置，如P1点、P2点、P3点等，观测的两个角度α、β均相同，亦即计算出的未知点的坐标也相同，但这在实际上是不可能的，是一件危险的事情，所以称这个外接圆就是危险圆。实际工作中要求测站点不仅不能摆在危险圆上，还要偏离危险圆的圆周一定距离，一般要偏离圆周R/5（R是危险圆的半径）的距离，要在图中的圆环范围以外设站。
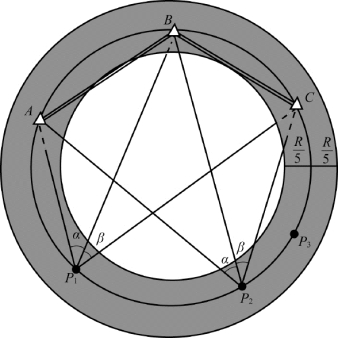
图7-31 后方交会的危险圆
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
