图7-11与前面介绍的图7-8(a)相同,是一种具有两个连接角的标准附合导线,也是一种较为经典的附合导线,在实际工作中颇受青睐。
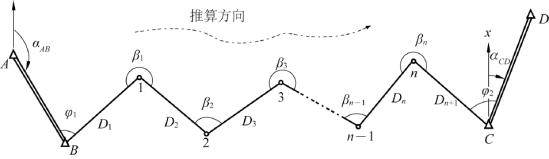
图7-11 附合导线计算示意图
1.方位角闭合差的计算与调整
项目2任务5已介绍了坐标方位角的概念,下面介绍坐标方位角是如何传递的。
(1)计算方位角与方位角闭合差。
先复习一下正反方位角与圆周角的概念:
①正反方位角:假定图7-11中已经计算出直线AB的方位角αAB,则已知起始点B所在的起始边BA的方位角为αBA,根据公式(2-9),有
![]()
正负号需根据实际情况进行选择,选择的依据只有一个:保证0°≤αBA≤360°。显然图7-11所示情况应该选“+”号。当然,如果是用计算机计算,则随意选择正负号也不会对后面的计算结果产生影响。
②圆周方位角:圆周角的度数为360°。针对图7-11,有
![]()
公式(7-2)的含义为:一条直线在加、减360°之后其方向不变。这里选择正负号的依据,也是保证0°≤αBA≤360°。用表格计算时需考虑正负号的选择,用计算机计算也可以不考虑。
方位角的推算原则为:前进边(未知边)的方位角,等于后续边(已知边)的方位角“+”或“-”这两条边的夹角,左角用“+”,右角用“-”。这里左角是指角度在前进边的左边,右角是指在前进边的右边,如图7-12和图7-13所示。该情况有点像经纬仪的水平角观测:顺时针旋转时方向值在增加,反之减少。
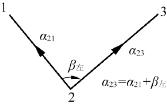
图7-12 方位角的传递——左角β左
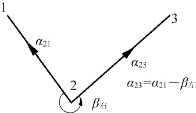
图7-13 方位角的传递——右角β右
【例7-1】 如图7-14所示,αAB=143°26′38″,αMN=34°16′33″,各观测角值如图7-14所示,试推算各未知边的坐标方位角。
[解] 图7-14(a)所示为沿前进方向进行左角观测,计算过程如下:
αBA=αAB+180°=323°26′38″,如取-180°则会小于0°;
αB1=αBA+260°13′24″-360°=223°40′02″,结果须减360°;
α1B=αB1-180°=43°40′02″,如取+180°则会大于360°;
α12=α1B+333°42′35″-360°=17°22′37″,结果须减360°;
α21=α12+180°=197°22′37″,如取-180°则会小于0°;
α23=α21+107°48′27″=305°11′04″。
图7-14(b)所示为两个小组分别从两端往中间观测(计算时出现了左、右角):
αM9=αMN+281°32′15″=315°48′48″;
α9M=αM9-180°=135°48′48″,如取+180°则会大于360°;
α98=α9M+245°35′07″-360°=21°23′55″,结果须减360°;
α89=α98+180°=201°23′55″,如取-180°则会小于0;
α87=α89-282°18′09″+360°=279°05′46″,结果须加360°。
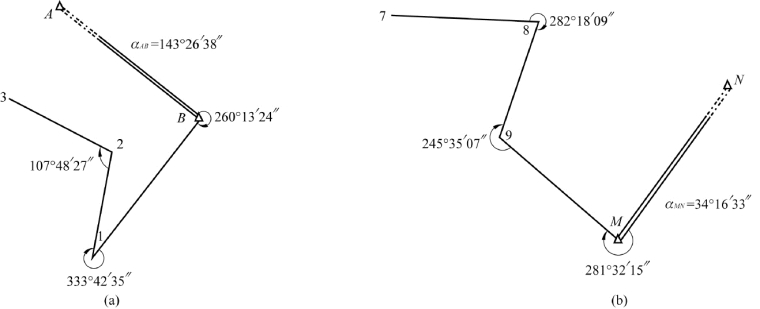
图7-14 坐标方位角的计算示例
其实,实际工作中采用图解法推算会更加直观准确。推算时按照“左角用+号,右角用-号”的原则。计算结果如图7-15所示。
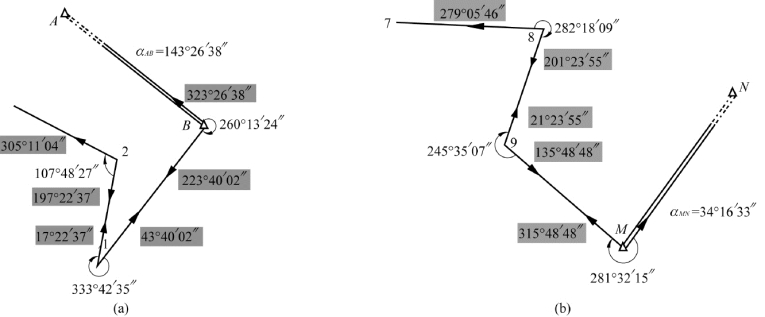
图7-15 方位角的推算
考虑图7-11中各观测角值均为左角,以及图中各导线边的实际方位情况,则导线各边的方位角推算如下:
如果将前面各条边方位角依次代入,则上式会变为(https://www.xing528.com)
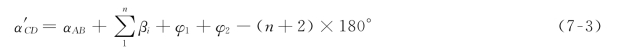
注意式(7-3)中的最后一项为(n+2)×180°,但该值并非一成不变,有时就会变为n×180°(相差一个圆周角),具体需根据实际情况而定。
式(7-3)中的α′CD是用导线所有的观测角值推算出来的,由于测角误差的存在,它与用C、D两点坐标根据公式(2-13)反算出来的方位角αCD存在差异:
![]()
fα就是导线测量的方位角闭合差,俗称角度闭合差fβ。
根据式(7-4)及式(7-3),有
![]()
取两倍中误差作为限差,即

若检核方位角闭合差未超限,则继续进行下面的工作。如果一个测区导线网中的导线数目达到10个,则还应根据公式(6-69)计算测角中误差,并保证测角中误差不超过GB 50026—2020中的相关规定(见图7-16)。如果仅仅是测量一条导线,则可以利用公式(6-51)计算测角中误差,并同样保证测角中误差不超过GB 50026—2020中的相关规定(见图7-16)。
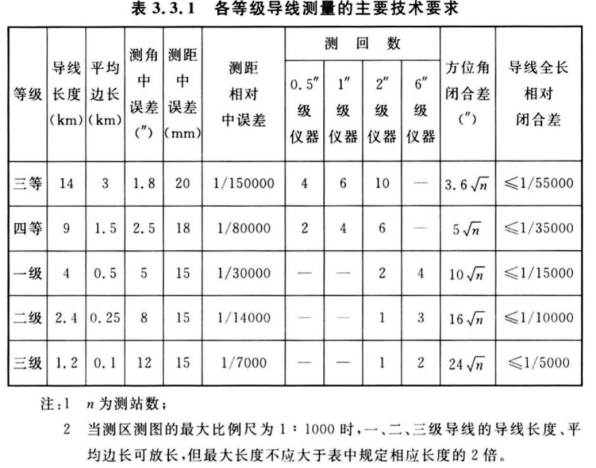
图7-16 GB 50026—2020《工程测量标准》规定的各等级导线测量主要技术要求
【分析思考】 公式(7-4)中α′CD的大小和精度与边长测量有关吗?
(2)分配方位角闭合差。
这项工作也称方位角闭合差的调整。由于各转折角都是按等精度观测,所以要将方位角闭合差fα平均分配到每个观测角度上(包括连接角),在式(7-3)中对n+2个观测角引入相同的改正数vα,有
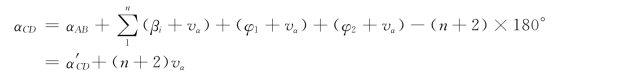
将式(7-4)代入上式,有

当观测角为右角时,其改正数为
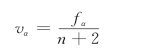
从而得到进行方位角改正之后的新的角度值。如果上面公式不能整除时,则将余数角度分配给短边所夹角的改正数中。分配时还应注意一个常识问题:分配的任何角度改正数都不能超过GB 50026—2020中的测角中误差规定值(见图7-16)。
2.坐标增量闭合差的计算与调整
将各观测角度进行方位角闭合差改正之后,便用新的角度值推算出每条导线边的方位角,再参照公式(2-11)计算出各条导线边的坐标增量:
![]()
式中,Di为观测各条边的水平距离,αi为用改正后的角度值计算出的各边方位角。
将图7-11中的各条边[共(n+1)条边]的坐标增量累加,理论上应满足如下条件要求:
![]()
但由于式(7-6)中还存在边长测量误差,故式(7-7)并不严格成立,而是存在一定误差,误差大小为
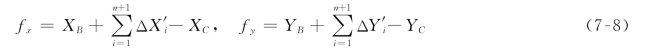
全长闭合差为
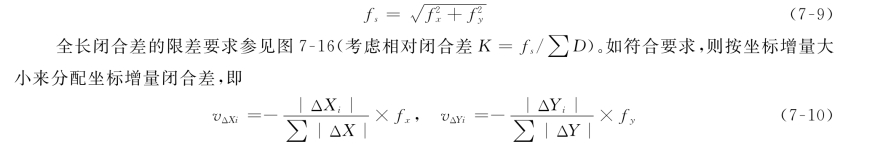
坐标增量分配完成之后,即可进行各导线点的坐标计算,注意最后计算出的C点的坐标应与原已知坐标完全一致。
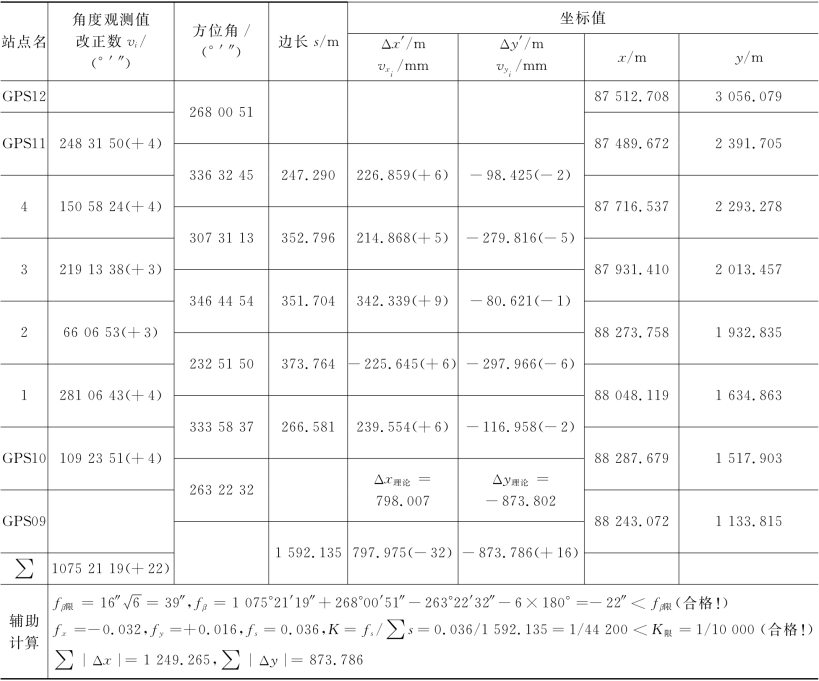
【例7-2】 图7-17为某二级导线测量示意图。已知4个控制点的坐标(见表7-2),观测出的6个角值和5条边长列于表7-2中,现要求按近似平差的方法进行导线计算,求出各导线点的坐标。
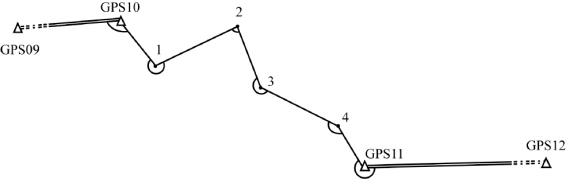
图7-17 导线测量示意图
[解] 此为标准的附合导线图形分布,4个未知点,5条观测边长,6个观测角值,有11-4×2=3个多余观测。导线测量的全部计算过程列于表7-2中。
表7-2 常用附合导线坐标计算表
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




