近似数运算结果及精度（测量基础与实训）

1.加、减运算

假设有四个凑整后的数字相加（比如四个小组各测一段距离然后相加）：

式中“？”表示该数在这一位上含有凑整误差。由这个算式可以看出，因为第二个被加数已经可能有0.05的误差，所以，运算结果最多能正确到小数点后第一位，小数点后第二位已经不可靠了，保留更多的小数位数是没有意义的。上述算式应该先进行凑整，再进行加法运算，改为

因此，在做加减运算时，凑整规则是，以小数位最少的那一数为准，其余各数和计算结果均凑整到比该数多保留一位。

多保留的一位数称为“安全数字”或“可疑数字”。上例运算结果有四位有效数字，最后一位数“2”为安全数字。

安全数字的保留与否，要看它是否还要继续参与计算，继续计算则应予保留，对于最终结果则可不保留。

和差计算结果的精度可按公式（6-2）估算。设n个近似数的和（或差）为Z=X1±X2±…±Xn，则

以公式（6-78）代入，有

将上述加法算式中四个数的极限凑整误差代入公式（6-80），算得

结果表明，和数696.82在整数位的中误差为0.029个单位，那么在小数点后第二位已有2.9个单位的中误差，因此，将结果保留到小数后第三位完全没有必要，但也不应只保留到小数点后第一位，因为在小数点后第二位数的凑整中误差并没有超过5个单位。

值得注意的是，应尽量避免两个彼此接近的数相减。因为相减的结果，有效数字可能大大减少，有效数字愈少，相对误差就愈大。当遇到这种情况时，要实事求是地认真对待，例如可改变计算公式避免使用减法计算。这一点，待分析乘除运算之后，再来举例说明。

2.乘、除运算

设要求两个近似数的积：A=223.12×0.33。

这两个近似数的末位是什么数字凑整来的，并不知道，现在用“？”号代替，于是将乘法写成如下形式：

由算式可见，乘积中第三个数字“6”已不可靠，保留更多的数字是没有意义的。这是因为两个乘数中的一个因子（0.33）只有两位有效数字，所以，乘积的有效数字最多只有两位。上例在计算时应该写为

得数为A=73.6。

对于近似数字相除来说，上述原则同样适用。于是，可以得出乘和除的凑整规则：在各因子中，以有效数字位数最少的为准，其余各因子及计算结果均凑整到比该因子多一位。这样，便可以避免做多余的计算工作。

【例6-21】　计算

分母中的103.293若机械地按上述规则凑整，那么应凑整到103，但根据近似数的相对误差来看，103和式中有效数字最少的0.083差不多，因而应该多保留一位，即取103.3。

【例6-22】　当θ=1°时，计算1-cosθ等于多少（1为常数，没有误差），并估算近似运算结果的精度。

［解］　若用六位数计算，则

若改变计算公式，同样用六位数计算，有

积（或商）精度可按公式（6-32）估算。

设有n个近似数的乘积为A=X1·X2·…·Xn，则

应用公式（6-80）代入上式，得

应用公式（6-81）计算乘法算式A=223.12×0.33，所得乘积的精度为

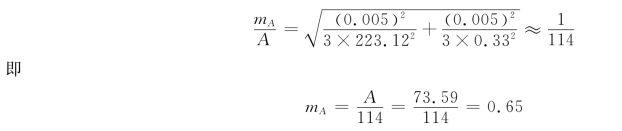
结果表明，乘积在整数位的中误差为0.65个单位，即在小数点后一位已有6.5个单位的中误差，因此，将结果保留到小数点后第二位就没有必要，只需保留到小数点后一位已够要求，即结果为73.6。

3.乘方与开方运算

对于乘幂Z=Xn，求其误差。

将上式微分，再与上式相除，得：

可见，乘幂的相对误差等于指数n与底数X的相对误差的乘积。若指数n=2，即平方时，平方值应凑整到与底数同样多位数的有效数字。若指数n=10时，则Z的取位应比X少一位有效数字。因此，乘方所得的结果比底数的精度低。

【例6-23】　求近似数8.98的平方值。

［解］　（8.98）2=80.6。

从这个例子可以进一步说明，若幂指数大于2而小于或等于10，则乘幂只需凑整到与底数同样多位数的有效数字，这实际上已保留了一位安全数字。

对于开方根，若有Y=，则(www.xing528.com)

【例6-24】　试计算86 456.883 9的平方根，求精确到5位有效数字的结果和精确到6位有效数字的结果。

［解］　根据开方根的凑整规则进行取位计算：

4.对数运算

对于对数Z=lg X=M ln X，式中M=1/ln10=lge=0.434294…，称为常用对数的模，简称对数模或对数率。

将上式对X取微分，有

即某数的常用对数的误差，等于该数本身的相对误差乘以对数模M。也可以说成，某数的常用对数误差，约等于该数本身的相对误差的一半（因为0.43近似等于0.5）。

【例6-25】　计算各近似数X1=0.40053，X2=200.46，X3=1.0435的对数及其误差。

［解］　由公式（6-84），得

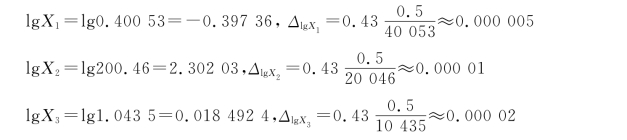
由上可以看出，当近似数的首位数近于4的时候，对数误差已达该近似数末位的0.5个单位，而首位数小于4时，误差更大。在极限情况下，当近似数首位数为1时，对数误差将达到末位的2个单位。

一般来说，根据对数表或用计算器进行计算时，应该至少使对数和近似数有效数字位数相同。而在近似数首位数小于4，尤其在小于2的情况下，应该使对数结果比原近似数有效数多一位。

5.三角函数

测量上常用的三角函数有正弦、余弦、正切、余切等四种，现取y1=sinα，y2=cosα，y3=tanα，y4=cotα。

将上列各函数式取微分，得

如果近似地取ρ=2″×105，则当角度误差为Δα=1″时，对于不同角度按公式（6-85）计算出相应三角函数值的误差，列于表6-7中。

表6-7　常用三角函数的误差

表6-7中数据表明：

（1）对于正弦函数来说，角度越小，由角度误差引起的函数值误差越大。除了84°以上的角度外，角度误差1″引起的函数误差都比六位函数表（或计算器的六位函数值）本身的极限凑整误差（5.0×10-6）大。因此，以秒（″）为单位的角度，其正弦函数值应该保留6位有效数字；

（2）对于余弦函数，角度愈大，由角度误差引起的函数误差愈大。除6°以下的角度外，角度误差1″引起的函数误差都比六位函数表本身的极限凑整误差大；

（3）正切和余切在任何情况下，角度误差1″引起的函数误差，都比六位函数表本身的极限凑整误差大。而且，角度越大，正切函数值的误差也就越大，余切函数的误差却越小；

（4）当用同样位数的函数表，由正切及余切函数反算角度，远比用正弦和余弦要好，因为用正弦（或余弦）反算角度，在该角度接近90°（或0°）时，若函数有小的误差存在，则将导致角度有较大的误差产生。

【例6-26】　设精确到厘米的坐标增量ΔX=440.00 m，ΔY=7.94 m，试用坐标反算公式计算坐标方位角及边长，并估算其计算精度。

［解］　（1）反算坐标方位角。

所以

将反算公式取对数，有

对上式取全微分，经化算后得

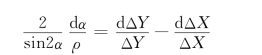
转换为中误差关系，得

所以

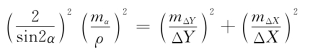
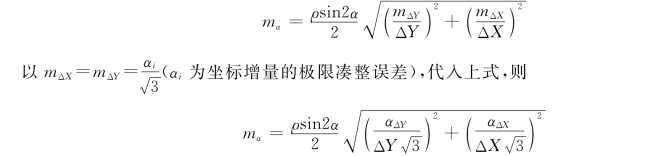
将已知数据代入上式，得

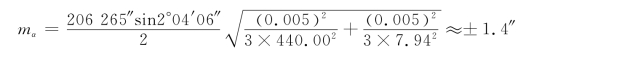
（2）反算边长。

①按ΔX计算，得

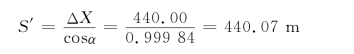
由公式（6-81）得：

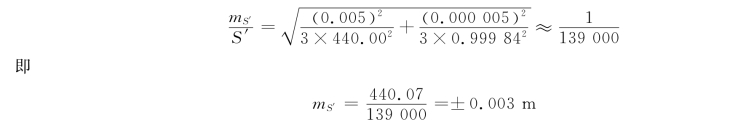
②按ΔY计算，得

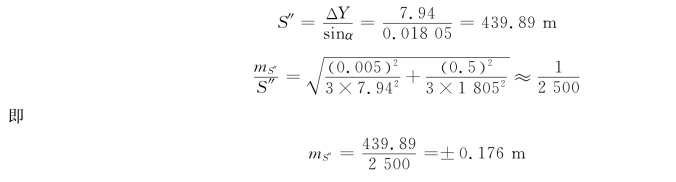
比较两种计算结果可知，按ΔX计算边长的精度高得多，原因是在上述小角度情况下，余弦函数比正弦函数的有效数字多。因此，当象限角近于0°时，用ΔX计算边长的精度高；相反，当象限角近于90°时，则用ΔY计算边长的精度高。所以，不加分析地取两个计算结果的中数是不对的，那样做往往会降低结果的精度。此例的结果应取前者，即S=440.07 m。当然，若采用勾股定理计算，则不论象限角的大小，其结果都是正确的。