测量基础与实训：凑整误差的四个特性

将同一类的大量随机凑整误差汇集在一起，从中可以总结出它们具有如下性质：

（1）凑整误差的绝对值不超过所保留的最末一位数的0.5个单位；（有界性）

（2）绝对值小于或等于极限凑整误差的各个误差出现的概率相等；（均衡性）

（3）绝对值相等的正凑整误差与负凑整误差出现的概率相等；（对称性）

（4）凑整到相同位数的n个凑整误差的算术平均值，随着n的无限增加而趋向于零。（抵偿性）

这些性质表明，凑整误差也是一种偶然误差。针对上述四个特性，可进行如下说明：

（1）凑整误差的第一个特性与一般偶然误差的第一个特性相类似，其区别在于凑整误差的极限值是个固定值；(www.xing528.com)

（2）偶然误差的第二个特性，是凑整误差没有的，即在误差分布上，它们迥然不同。对于凑整误差来说，凡在极限凑整误差范围内的所有可能出现的凑整误差值，出现的概率都是相同的。例如，当考虑一列由精确到小数点后一位的数凑整为整数时，以整数的个位数为单位，可以写出它们的凑整误差可能为

-0.5，-0.4，-0.3，-0.2，-0.1，0，+0.1，+0.2，+0.3，+0.4，+0.5

所有这11个误差，出现的概率都相同（均为1/11）。这就是说，凑整误差按绝对值分布，在0～0.5的范围内是均匀的。因而，凑整误差具有均匀分布的性质。图6-13形象地表达了凑整误差的这种均匀分布情况（图中的误差值以凑整数据的末位数为单位）。由此也说明，不是所有偶然误差都服从正态分布。

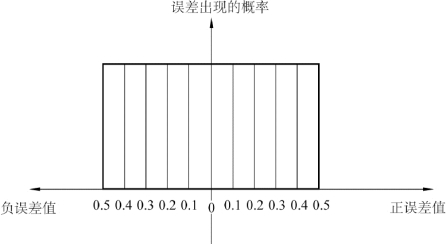
图6-13　凑整误差的均匀分布图

（3）凑整误差的第三和第四特性，与偶然误差的第三和第四特性相同，说明凑整误差也具有抵偿性。