测量基础与实训：权的计算方法及应用

实际工作中，除了上述的等精度观测以外，经常也会出现不等精度观测的情况。例如，从三个已知水准点出发，沿三条不同长度的水准路线测定某未知点高程，分别测得的三个未知点高程便是不等精度观测值，这时就不能简单地取三个高程的算术平均值作为最后结果。

于是，就需要引入“权”的概念来处理类似问题。

测量误差理论中，以p表示权，并定义观测值（或函数值）的权与其中误差的平方成反比：

式（6-53）说明某个观测值或函数值的中误差m越小（精度越高），其权越大，反之亦然。权也可以像中误差那样体现观测值的精度。式中c为一任意正数。

通常定义数值等于1的权为单位权，权等于1的观测值为单位权观测值，权等于1的观测值的中误差称为单位权中误差，单位权中误差用μ（有时用m0）表示。注意，单位权的值肯定等于1，但单位权中误差的值却不一定等于1。

由于式（6-53）中的c可以是任意正常数，因此引入单位权中误差之后，权也可以表达为

中误差的另一种表达式为

式（6-55）表明，在知道单位权中误差的前提下，求取任何值的中误差就变成了计算相应值的权。实际上，计算一个未知量的权要比直接计算这个量的中误差要容易。因此公式（6-55）通常用来求取观测值的中误差与观测值的函数值的中误差，以及用来评定整个测区的观测精度质量。

在设计单位权（定权）时，一般取一次观测的中误差（角度测量）、单位长度的观测值中误差（距离测量、水准测量）、一测站观测值的中误差（水准测量）等作为单位权观测中误差。下面是一些定权的示例。

1.不同测回观测时角度测量的权

根据上述单位权μ的含义，可定义一测回水平角观测值的权为单位权（p0=1），则一测回的水平角观测值的中误差μ就是单位权中误差，根据误差传播定律，N测回的水平角中误差为

代入式（6-54），N测回水平角观测值的权为

即一测站角度测量的权与角度测量的测回数成正比。测回数越多，观测结果的精度越高。

2.导线测量中方位角闭合差的权

先考虑图6-11（a）所示附合导线，设导线观测了n个内角，则该导线方位角闭合差为

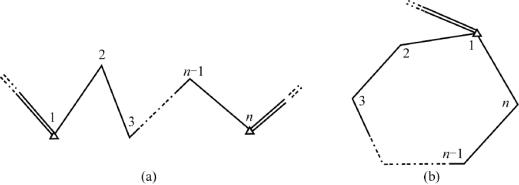
图6-11　附合导线与闭合导线示意图

由于各个角均是等精度观测，则根据误差传播定律，有（这里不考虑α始、α终的误差）

可定义每个角的观测中误差mβ为单位权中误差μ，于是有

这说明导线测量时，方位角闭合差的权与导线的角度个数成反比。角度越多，角度累积的误差越大。

对于图6-11（b）所示闭合导线的情况，根据多边形内角和的公式，同样可推得上述结论。(www.xing528.com)

3.水准测量的权

可取1 km路线的高差测量中误差μ作为单位权中误差，参见公式（6-34），则线路长度L（单位为km）的高差测量的中误差为

按式（6-54），线路长度L的高差测量结果的权为

即线路水准测量的权与路线长度成反比。路线越远，水准测量积累的误差越大。

如果是崎岖山路水准测量，测站数较多时，可取一测站的高差的权为单位权，则一测站的高差中误差为单位权中误差，同理可推得n测站的高差值的权为

即山区线路水准测量的权与测站数成反比。测站数越多，测量结果的精度越低。

4.距离测量的权

钢尺量距时，根据尺段累加测得起点到终点之间的距离，因此可取1单位（如以100 m或1000 m为1单位）距离测量的权为单位权，类似水准测量误差传播的方法，可推得L倍单位长的距离测量的权为

即钢尺量距测量结果的权与所量距离成反比。

对于光电测距，也可参照式（6-60）定权。

5.三角高程测量的权

忽略三角高程测量中的一些小误差改正影响，三角高差在原理上的主项是h=D sinα，应用误差传播定律，高差中误差为

式中，mD是测距误差；mα是垂直角测量误差。

参照例6-13中的等影响原则分析，将（D×mα）2看成与mD2同级别影响，而三角高程测量时一般取α＜5°，相比之下，sin2α≪cos2α（如果用α=10°代入，二者已相差31倍），故上式可以表达为

即

观察（b）式，可设距离为1单位的高差中误差为单位权中误差μ，即即三角高程测量的权与所测倾斜距离的平方成反比。

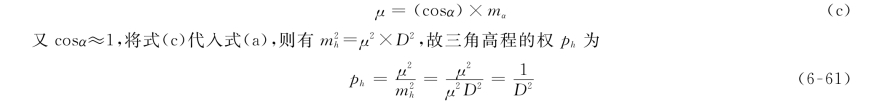
将式（c）代入式（b），可得三角高差测量的中误差计算公式为

当然式（6-62）也可从式（6-61）中直接获得。

应用时注意上式与水准测量中误差的计算公式（6-34）的区别。水准测量的高差中误差与距离的平方根成正比，而三角高差的测量中误差与距离成正比。显然在三角高差测量中距离对误差的影响比在水准测量中要厉害得多。