【摘要】:将公式变形,有式中各观测值相互独立,可应用误差传播定律,得算术平均值的中误差为可以对式进行验证,当观测次数n在10以内增加时,M减小的倍数很快,当n在10以上增加时,M减小的倍数相对较慢,n越大,其算术平均值提高精度的趋势也就越慢。求其算术平均值及其中误差。表6-4按观测值的改正数计算中误差
将公式(6-46)变形,有
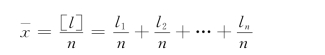
式中各观测值相互独立,可应用误差传播定律,得算术平均值的中误差为

可以对式(6-52)进行验证,当观测次数n在10以内增加时,M减小的倍数很快(算术平均值的精度迅速提高),当n在10以上增加时,M减小的倍数相对较慢(算术平均值的精度提高幅度不大),n越大,其算术平均值提高精度的趋势也就越慢。所以,实际工作中并不是观测次数越多越好,一般考虑经济原因而对观测次数有一定限制,通常规定重复观测次数不超过12次。限制观测次数的另一个原因是,无法用单纯重复观测的方法消除某些系统误差的影响,因为如果重复观测次数过多,则会使计算结果的精度掩盖系统误差的影响,导致错误的精度结果。例如,用一把毫米刻划的钢尺往返量测某段距离(称一测回),测量其结果的相对误差约为1/5 000的话,则测9个测回可将相对精度提高为1/15 000,这是比较可行的。但如果测900个测回,按误差传播定律可将其精度提高为1/150 000,这当然就是不可行的了,因为系统误差的存在大大掩盖了结果精度的真实性。(https://www.xing528.com)
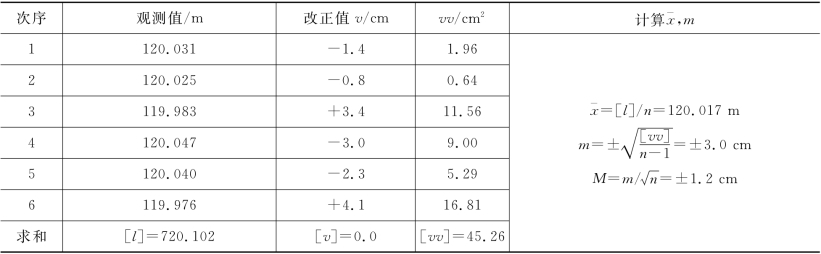
【例6-14】 在相同条件下对某一水平距离进行6次观测,观测数据见表6-4。求其算术平均值及其中误差。
[解] 先按式(6-46)计算6个观测值的算术平均值,再按式(6-47)计算各观测值的改正数,接着计算改正数的平方数,最后按式(6-50)及式(6-51)计算观测值及算术平均值的中误差。计算过程列于表6-4中。
表6-4 按观测值的改正数计算中误差
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




