误差共同影响原则及实践-《测量基础与实训》

1.各独立偶然误差的共同影响原则

在测量实践中，经常会遇到一个观测结果同时受到许多独立偶然误差共同影响的情况。例如，水准测量时，高差观测值会受到仪器误差、瞄准误差、读数误差以及其他误差的共同影响。在这种情况下，观测结果的真误差就是各个独立误差的代数和，即

由于这些真误差在数值和符号上都具有偶然误差的性质，且是相互独立的，所以与和差函数的情况相同，则其中误差关系为

即一些独立误差引起的观测值中误差的平方，等于各独立误差中误差的平方和。

【例6-12】　水准测量时，一次读数同时受到气泡整平误差、照准误差、估读误差以及水准尺刻划误差等的共同影响。若设m整平=±1.2 mm，m照准=±0.8 mm，m估读=±0.5 mm，m分划=±0.3 mm。试求一次读数的中误差m读。

［解］　按公式（6-39）得

即

2.偶然误差与系统误差的共同影响原则

通常，测量结果不仅带有偶然误差，在某种程度上还包含有系统误差。尽管我们在观测过程中，对系统误差总是设法加以消除或减弱，使得结果中的系统误差居于次要地位。然而，系统误差影响不是经常可以预知，并能够从观测结果中完全消除的。有时，即使某些测量的系统误差可以测定，也不能使它完全消除。因此，观测结果中往往还会含有残余系统误差的作用。在这种情况下，便有必要研究既含有偶然误差，又含有残余系统误差的观测值的精度。

设有同一个量的n个等精度观测值之真误差为Δ1，Δ2，…，Δn，且每一真误差都包含有偶然误差和系统误差。现以εi表示真误差Δi的偶然误差部分，以λi表示系统误差部分，则可写出对上式中每一等式的两端取平方，相加并除以n，得

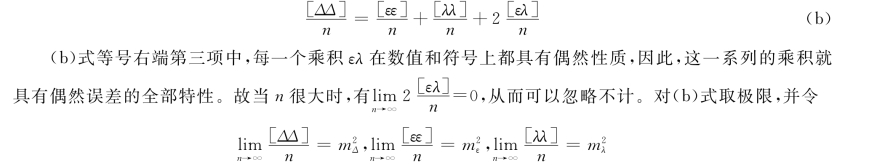
即得

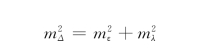
或

式中，mΔ为观测值的中误差，mε为偶然误差部分的中误差，mλ则为系统误差部分的中误差。

由此得出结论：在偶然误差和系统误差的共同影响下，观测值的中误差等于偶然误差影响中误差和系统误差影响中误差的平方和的平方根。

3.等影响原则

以上所述都是根据观测值的精度求算观测值函数的精度。但是，在测量实践中经常有这样的情况，事先给定函数值的精度，要求预先估计各观测值应达到的精度。(https://www.xing528.com)

根据已知函数z=f（X1，X2，…，Xn）及给定的精度mz来求观测值的精度m1，m2，…，mn，通常采用等影响原则。等影响原则就是假定各观测值对函数的中误差具有相同的影响，也就是假定公式（6-39）右边所有的各项都相同。即

这样，便可计算出m1，m2，…，mn的值，再根据实际工作的需要与可能，做精度调整，即人为地进行精度分配，最后确定出各观测值实际应达到的必需精度。

【例6-13】　如图6-9所示，要求在已知点B上用极坐标法进行放样测量，使P点的点位误差小于±5 cm。若s=200 m，试问要用什么样的精度来测定角度β和距离s。

［解］　图中A、B均为已知点，用极坐标法放样时，测量角度β与距离s可以获得P点的位置。测量时由于测角误差Δβ和测距误差Δs的存在，使得点位发生偏移至P′点（见图6-10）。

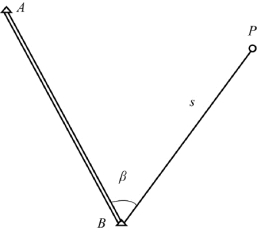
图6-9　点位放样

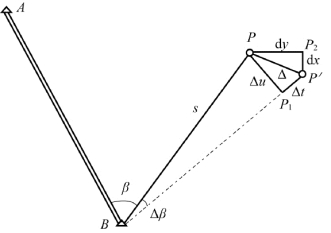
图6-10　点位误差的等影响原则应用

点位误差Δ可看成是横向误差Δu与纵向误差Δt的共同影响（按坐标增量计算时，也可以看成是两个坐标增量误差d x、d y的共同影响）。由于Δu、Δt相对于s来说均是一个很小值，可以将Δu当成是测角误差Δβ所对应的圆弧值，同时又与Δt、Δ构成直角三角形的三条边，即有

仿照例6-10，将（c）式换成中误差，有

如果按坐标增量放样，同样有

根据上述等影响原则，令式（6-42）右边两项相等，有

即为了使P点的点位误差达到5 cm的要求，需要用1/5700的相对精度量距，±36″的精度测角。

为了使各观测值既能满足设计精度要求，又不盲目地追求不必要的高精度而造成资源浪费和经济浪费，还应对计算结果实事求是地分析，并进行灵活处理。如对上例情况来说，现在角度的精度要求还不是很高，提高角度观测的精度比提高钢尺量边的精度就容易一些，故可适当提高测角精度，若使m=±15″，则量边精度可降低到

由此可看出，将按等影响原则所给出的结果做比较，用逐渐改变各观测值中误差的方法，可以使它们达到既经济又合理的配合。