测量基础：一般函数及误差探究

一般函数可表达为

式中，x1、x2、…、xn为独立观测值，其真误差相应为Δx1、Δx2、…、Δxn。

于是有z+Δz=f（x1+Δx1，x2+Δx2，…，xn+Δxn）。

由于Δxi是一个微小量，故上式可按泰勒级数展开。在展开式中取Δxi的一次幂项，有

将式（6-31）代入上式，有

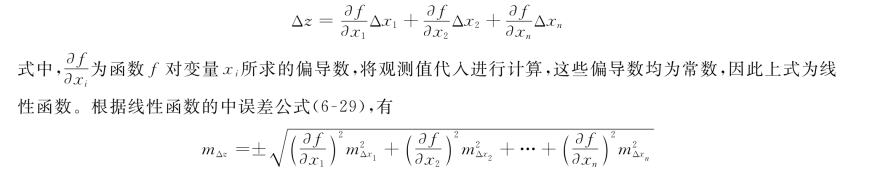
上式是函数真误差的中误差。分析式（6-1）可知，由于真值没有误差，因此观测值真误差的中误差也就是观测值本身的中误差，即有

故一般函数的中误差，等于该函数对每个独立观测变量取偏导数与相应变量中误差乘积之平方和的平方根。

式（6-32）具有普遍意义，是误差传播定律的通用形式，前面的和差函数、倍函数、线性函数，均是式（6-31）的特例，并能由式（6-31）直接导出。

【例6-8】　矩形面积公式S=ab，设矩形边长分别为a±ma、b±mb。求矩形面积S的中误差。

［解］　对于S，直接利用公式（6-32），有

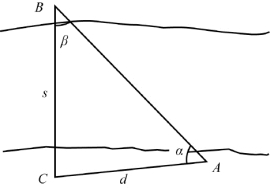
图6-6　求河流的宽度

【例6-9】　如图6-6所示，为了获得河流的宽度s，沿河边测量距离d的中误差为md，测量角度α、β的中误差分别为mα、mβ。求河流宽度s及其中误差。

［解］　应用正弦定理，得

分别对各自变量求偏导数：

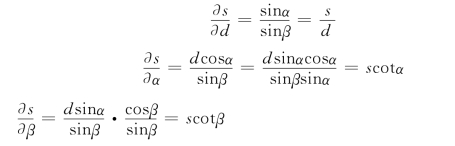
代入式（6-32），有

下面的例6-10省略求偏导数的具体过程，直接将全微分转换成中误差的形式，得到的结果相同。

【例6-10】　野外工作时经常在已知控制点上用支导线支出一个待定控制点P计算其坐标，按两点间的坐标方位角α和水平距离s计算坐标增量Δx和Δy，然后加上已知点坐标得到待定点坐标，如图6-7所示。设观测值α和s的中误差分别为mα和ms，试计算坐标增量中误差mΔx、mΔy，以及点位中误差mP。

［解］　坐标增量的函数关系式为

图6-7　用方位角、边长计算坐标

对上式求全微分，得到

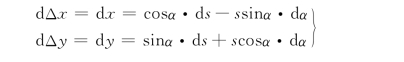
化成中误差的表达式：

参见图6-7，当不考虑已知点的误差时，未知点P的点位误差d P可看成是两个坐标增量误差d x、d y的共同影响，即有

将上式换成中误差形式：

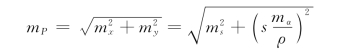
上式最右端根号内第一项为两点间的纵向误差，第二项为横向误差，即两点间的距离误差形成纵向误差，方位角误差构成横向误差。

【例6-11】　试分析水准测量规定的各项限差缘由。

［解］　针对水准测量的精度表达与限差要求，可做如下几项分析。(www.xing528.com)

①分析水准测量的路线高差中误差与测站高差中误差的关系。

为了测量AB两点间高差，用了n个测站，即

只要观测方法不变，观测条件基本稳定，一般认为各测站观测是等精度观测。设各站高差观测中误差为m站，对上式应用误差传播定律，有

可见，线路水准测量的高差中误差与测站数的平方根成正比，因此，实际中在满足要求的前提下，可以加大视距以减少线路的总测站数。

对于平坦地区，可设n=L/s，其中L是水准路线总长，s是一测站的前后视线长度，L、s均以千米为单位。于是有

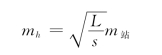
以L=1 km代入上式，得1 km的观测高差中误差为

即有

可见，线路水准测量的高差中误差与线路长度的平方根成正比，因此，实际中对于水准线路的长度应有所控制。例如，GB 50026—2020规定，四等水准路线长不能大于16 km，如图6-8所示。

图6-8　GB 50026—2020《工程测量标准》技术要求

②分析线路水准测量中闭合差的限差要求选择方式。

水准测量中，测段往返测互差、附合水准路线的附合差、闭合水准路线的闭合差等各种水准路线均有限差要求，如GB 50026—2020《工程测量标准》对四等水准测量中的往返较差、附合路线或环线闭合差Δh（单位为mm）有如下规定：

平地：

山地：

如将上两式相减，并取L=1 km，可算得n≈11（站），这说明如果1 km往返观测11个测站时（相当于每测站前后视距之和约为90 m），选择上面两个公式中的哪一个进行限差要求没有什么区别；如果各测站平均视距大于90 m时，n＜11（站）选择用式（6-35）要求较为宽松；如果是非平缓地带，测站平均视距小于90 m时，n＞11（站）则选择式（6-36）作为限差要求较容易达到。而GB/T 12898—2009《国家三、四等水准测量规范》则明确规定山区水准测量时的附合路线或环线闭合差限差为±25 mm。

③分析水准测量中各项限差的相互关系影响。

式（6-38）表明每千米观测高差中误差与测站的视线平均长度的平方根成反比，当每测站的视线平均长度增加时，每千米的测站数量会相应减少，从而单位长度（1 km）的高差测量精度会有所提高。

图6-8中第一项技术要求就是针对各等级的水准测量每千米高差全中误差的限差要求（例如对四等水准的要求为10 mm）。同样按2倍中误差的限差考虑，可认为四等水准测量的每千米高差全中误差为5 mm，即μ=±5 mm。

将μ=±5 mm代入式（6-38），有

这是四等水准测量中一测站的平均视距长度的基本考虑。当然，实际中为提高工作效率和降低每千米测量中误差，视线长度会有所增加。但如果视线过长又会产生其他方面的影响，如读数误差等，所以同时规定四等水准测量使用的DS3仪器，视线长度不能超过100 m。

④分析水准仪型号所代表的实际意义。

水准仪的型号如DS05、DS1、DS3等，其数字指水准仪能达到的每千米往返测高差中数的中误差（单位为mm），如DS3就代表该水准仪每千米往返测高差中数的中误差为3 mm。水准测量中的高差中数

设往返测精度相等，则高差中数的中误差为

即

上式表示，对于某一确定水准仪，1 km水准测量各测站中误差与1 km之内的测站数成反比。

如对于DS3水准仪，限差为3 mm，中误差则为1.5 mm，于是：