测量基础与实训：精度评估指标

1.中误差

为了衡量在一定条件下观测结果的精度，用标准差σ作为指标是比较合适的。但是，在实际测量工作中，不可能对某个量做无限多次观测，因此，在测量中定义按有限次观测的偶然误差求得的标准差为中误差，用m表示，即

式（6-7）又可简述为：中误差是偶然误差平方和的平均值的平方根。

用中误差m代替式（6-4）中的标准差σ，则正态密度函数可表达为

【例6-1】　现分甲、乙两组对10个三角形的内角进行观测，将各组测得的三角形的内角和观测值列于表6-2，现要求计算各组的三角形内角和观测值的中误差。

［解］　这里三角形内角和有其真值为180°，计算各观测值与真值的差值即为各观测值的误差且是真误差，同时计算各观测值误差的平方并求和，一并列于表6-2中。

表6-2　三角形内角和的中误差计算

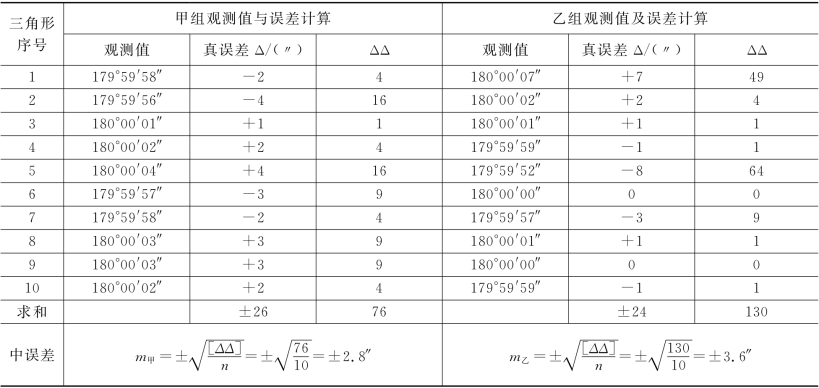
由表6-2可以看出，乙组观测值的中误差m乙大于甲组观测值的中误差m甲，即乙组的观测精度较甲组要低。这主要是乙组观测值中出现了两个较大的误差（+7″，-8″）。

在一组观测值中，如果标准差已经确定，就可以绘出它所对应的偶然误差的正态分布曲线。根据式（6-8），当Δ=0时，f（Δ）有最大值，最大值为

当m较小时，曲线在纵轴方向的顶峰较高，在纵轴两侧迅速逼近横轴，表示小误差出现的频率较大，误差分布比较集中；当m较大时，曲线的顶峰较低，曲线形状平缓，表示误差分布比较离散。以上两种情况的正态分布曲线如图6-4所示（图中的m1与m甲相对应，m2与m乙相对应）。

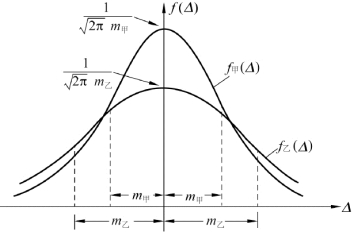
图6-4　不同中误差的正态分布曲线

2.平均误差

在一定的观测条件下，偶然误差绝对值之算术平均值的极限，称为平均误差，用θ表示，即

用或然率理论可以证明，当n→∞时，按式（6-9）计算的平均误差θ可以正确地衡量观测值的精度。但是，实际中的观测次数是有限的，只能用下式计算平均误差，即

【例6-2】　针对表6-2中的两组观测值，用平均误差评定其精度情况。

［解］　利用表6-2中的真误差求和结果，应用式（6-9），其平均误差分别为

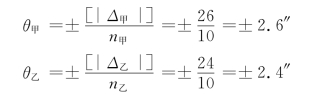
此结果表明，甲组的观测精度较乙组稍差，这说明当观测次数不够多时，用平均误差衡量精度会掩盖那些较大误差（如大于两倍中误差的误差）对观测质量的影响。

3.或然误差

在英、美等国家中，也有用或然误差来评定精度的。或然误差是将一系列等精度观测值的误差按绝对值大小排列，取其最居中的一个来作为衡量精度的标准，用符号ρ表示。若观测的误差数为偶数，则取中间两个误差的平均值。

【例6-3】　用或然误差评定表6-2中两组观测值的精度。

［解］　将两组观测值的误差按绝对值从小到大排列如下：

甲组：+1，-2，-2，+2，+2，-3，+3，+3，-4，+4

乙组：0，0，-1，-1，+1，+1，+2，-3，+7，-8

则有ρ甲=±2.5″，ρ乙=±1.0″。

与表6-2中误差的计算结果相比，也得出了相反的结论。这也是观测次数还不够多的缘故。

对于上述三种衡量精度的指标（中误差、平均误差、或然误差），可以根据概率理论进行证明，当观测次数足够多时，它们之间存在如下的关系式：

事实上，那些采用或然误差作衡量精度标准的国家，通常也是先计算中误差，然后用式（6-12）来确定或然误差^[2]。

前面已经知道，误差分布曲线的表达式（密度函数）的唯一参数就是标准差σ，确定的标准差对应确定的分布曲线。而标准差的估值是中误差，于是也可认为一定的中误差也有一定的误差分布曲线相对应，因此中误差能够作为衡量观测精度的指标。再根据式（6-11）和式（6-12）可知，不同的θ或ρ值也对应着不同的误差分布曲线，因此平均误差θ、或然误差ρ也可以作为衡量精度的指标。这就是说如果观测次数足够，用上述任何一种指标进行精度衡量都是可靠的。

但当观测次数不太多时，用中误差衡量就比较可靠，其原因分析如下。

（1）中误差利用各项误差的平方进行累加计算，能灵敏地反映大误差的影响，而大误差（接近粗差）对测量结果的可靠程度起决定性影响；(www.xing528.com)

（2）中误差比较稳定。通常只需要不太多的观测次（个）数，就能用中误差对观测质量进行准确评定。由概率理论可以证明，确定中误差本身的中误差可按下式①计算：

式中，n为实际的观测次数。式（6-13）表明确定观测值中误差的中误差与观测次数n的平方根成反比。取不同的n值代入式（6-13），计算的结果列于表6-3。

表6-3　确定中误差的中误差

从表中可以看出，如已有4次观测，则确定该中误差的相对误差为0.35，即有65%的可靠度；当有10次观测时，可靠程度达78%，因此标准规定一般要有10次（个）以上的观测才能进行中误差的计算。

4.极限误差

根据偶然误差的第一特性——有界性，当观测误差超出一定范围时，说明观测条件发生了突变。因此，为了保证观测质量，必须对误差的界限进行讨论研究，这就是考虑极限误差大小取值的问题。严格来说，极限误差并不是一种衡量观测值精度的指标，而是一种保障观测精度所采取的措施。

由图6-1所示误差分布直方图可知，图中各矩形面积大小反映误差出现在该区间内的频率。当误差的个数无限增加、误差区间又无限缩小时，频率逐渐趋于稳定而演化成为概率，致使直方图的顶边形成正态分布曲线。因此，根据正态分布曲线，误差出现在某微小区间dΔ内的概率可表示为

要得到偶然误差在任意区间内出现的概率，对上式进行积分便可。

设以纵轴两边k倍中误差范围作为误差区间，则在此区间内误差出现的概率为

分别以k=1，k=2，k=3代入式（6-15），可得到偶然误差的绝对值不大于1倍中误差、2倍中误差、3倍中误差的概率分别为

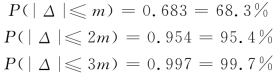
由此可见，对于一定条件下的大量观测值，偶然误差有68.3%都是出现在中误差范围以内，大于2倍中误差的约占误差总数的4.6%，而大于3倍中误差的仅占误差总数的0.3%。一般进行的测量次数是有限的，2倍中误差应该很少遇到，因此，可以按2倍中误差作为允许的误差极限，称为允许误差，简称限差，即

有些国家采用3倍中误差作为极限误差。我国现行测量规范中一般取2倍中误差作为限差。超过2倍中误差的观测值摒弃不用，应返工重测。

偶然误差出现在2倍中误差之内的概率为0.954，这相当于在误差分布曲线中，在-2m至+2m之间的误差范围内，曲线与坐标横轴所包含的面积数值为0.954，如图6-5所示。

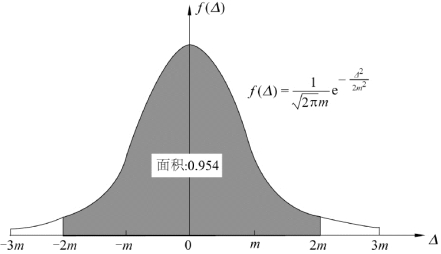
图6-5　误差曲线中2倍中误差以内的概率

大量统计调查也表明，在Δ误差群中，超出2m的Δ约占5%；超出3m的Δ仅占0.3%。大量的Δ均不会超过2m。由此也可认为，误差Δ超出2m的观测值，是含有粗差的不正常观测值。这样，规定Δ≤Δ允=2m，便可起到发现和限制粗差、保证观测质量的作用。

5.相对误差

前面介绍的真误差、中误差、平均误差、或然误差等，都是绝对误差，是有测量单位的。在很多实际测量工作中，有时只用绝对误差还不能完全表达观测质量的好坏。例如，丈量某一长度的中误差为±1 cm，如果不知道该长度的大小，还是无法判断该测量结果的精度高低，如若±1 cm是丈量300 m长的直线的精度，当然可认为该测量精度是较高的，如若是测量3 m长标杆的精度，则认为该测量精度是较低的。类似的情况我们在土地面积测量、土石方体积测量中也经常遇到。

一般地，我们用观测值的中误差与观测值本身的比值作为该观测值的相对误差。对于长度、面积、体积测量，其相对误差计算公式可依次表达如下

实际工作中，由于观测次数不够，中误差是无法知道的，通常就用绝对误差来代替。例如，导线测量时对导线全长闭合差的要求便是如此。

相对误差没有单位。通常将相对误差化成分子为1的分数形式，有时也化成百分比。实际中当上面各式中的中误差无法求得时，可用其他误差代替，如较差、平均误差等，而分母尽可能用最或然值。分数形式的相对误差的分母，通常只需在左端保留2～3位不是零的数字，其余均用零代替。凑整时只能舍去不能进位。

相对误差中也有极限误差的要求。如GB 50026—2020《工程测量标准》规定的一级导线距离测量相对中误差不能超过1/30 000，导线全长相对闭合差的极限误差为1/15 000。显然，相对误差可以作为一项指标去衡量不同项目观测精度的高低，同时相对极限误差又可以作为一种措施标准使测量精度得到有效控制。

【例6-4】　某地区规划设计两地块的围海造田工程，甲地块设计面积500 000 m2，要求填沙1 500 000 m3，乙地块设计面积1 000 000 m2，要求填沙3 000 000 m3。两地块的工程分别由甲、乙两单位投标完成。工程竣工验收时，精确测量出甲地块实际面积为488 866.8 m2，填沙量为1 456 600.4 m3，乙地块实际面积为981 865.5 m2，填沙量为2 883 596.5 m3。现评估两项工程的施工精度。

［解］　这里的规划设计值可视为真值（理论值），由于施工方的测量、施工误差，导致实际结果与理论值不符，其面积绝对误差、相对误差，体积绝对误差、相对误差分别为

地块甲：

地块乙：

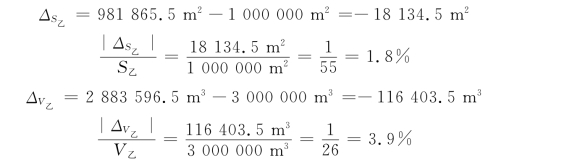
可见，甲地块的面积范围施工精度较乙地块要低（2.2%＞1.8%），但填沙土方量的工程精度较乙地块要好（2.9%＜3.9%）。