测量基础与实训：直方图和误差分布曲线分析

描述误差分布的情况，除了用上述统计表格的形式表达外，还可以用图形来表达。设误差的总个数为n，出现在某一区间的个数为k，则k/n为误差出现在该区间内的相对个数。以横坐标表示误差值的大小Δ，纵坐标表示各区间内误差出现的相对个数k/n与区间的间隔值dΔ（如上例中的间隔dΔ=1″）的比值，这样，每一误差区间上的长方形面积就表示误差出现在该区间内的相对个数，相对个数的总和等于1，即直方图中所有长方形面积的和等于1。图6-1所示是根据表6-1绘制出的误差分布直方图。

设想使n→∞，同时使误差区间dΔ无限缩小，直方图中的长方形顶边所形成的折线，将成为一条光滑的曲线，该曲线就是误差分布曲线，如图6-2所示。

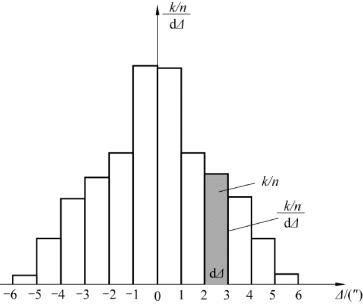
图6-1　误差分布直方图

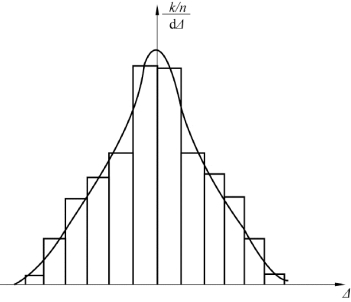
图6-2　误差分布曲线

实践证明，当n足够大时，一定的观测条件对应着一种确定不变的误差分布曲线。如果用不同观测条件所对应的误差分布曲线进行对比，可以判断出它们彼此之间的观测结果的精度高低。若曲线形状比较陡峭，表示接近于零的小误差出现的概率较大，误差分布较为密集，观测精度较高；若曲线形状比较平缓，表示接近于零的小误差出现的概率较小，误差分布较为离散，观测精度较低。

在概率统计理论中，当n→∞时，图6-2所示的误差分布曲线又称为正态分布曲线，它准确地表示了偶然误差出现的概率P，即说明在上述各误差区间内，误差出现的频率趋于稳定，逐渐演化成误差出现的概率。(https://www.xing528.com)

偶然误差服从正态分布，正态分布又称高斯分布、常态分布。其数学方程式是

式中，圆周率π≈3.14159，自然对数的底e≈2.71828，Δ为观测值的误差（系统误差可忽略，以偶然误差为主），σ为标准差，用公式表示为

标准差的平方σ2称为方差，表示为

式（6-4）称为正态分布的密度函数，函数以偶然误差Δ为自变量，以标准差σ为唯一参数。还可以证明，当Δ=±σ时，二阶导数f″（Δ）=0，由此判断-σ、+σ是误差曲线两个拐点的横坐标值。