水平距离投影面的斜距测量与改化

距离测量有平距与斜距之分。斜距为任意两点之间连线的长度，这是比较直观的概念。但对于水平距离，由于我们的测量活动是在地球表面进行的，还定义了水准面及参考椭球面，因此，有必要继续定义水平距离为斜距投影到某高程面（如大地水准面或参考椭球面）上的长度^[1]。不过大地水准面是一个千变万化、无法捕捉的复杂曲面，我们便用参考椭球面来代替它。但实际中到底是用参考椭球面还是用某一具体选定的高程面，下面的分析将给出答案。

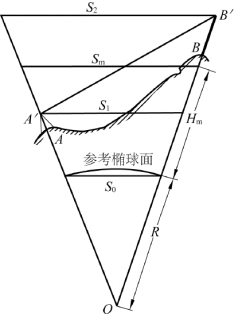
图5-1　距离在水准面上的投影

在图5-1中，先要假设仪器铅垂线指向参考椭球体的中心（其影响大小将在本项目任务5中介绍）。图中设A、B为地面上两点，仪器A′瞄准目标B′测量的斜距为d，d在过仪器中心A′点高程面上的投影长度为S1（此处以直线长度代替曲线长度，下同。至于用弦线代替弧线的误差，也将在本项目任务5中详述，这里先给予忽略），在过瞄准点B′高程面上的投影长度为S2，在参考椭球面上的投影长度为S0，从图中可见，S1≠S2≠S0，即地面上两点连线在不同高程面上的投影长度是不相等的。

设S1和S2的平均长度为Sm，其平均高程为Hm，地球曲率半径为R，由图可知

即

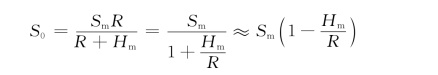
则距离误差为

这里的ΔS就是水平距离的投影面改正，又称海平面改正（从平均高程面到平均海水面的改正）。

相对误差为(www.xing528.com)

如果要求距离误差不超过其长度的1/T，即

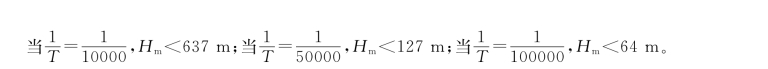
这就是说，当要求距离误差不超过1/10000、1/50000和1/100000时，只要边长的平均高程分别不大于637 m、127 m和63 m时，可认为S0=Sm，能够直接用大地水准面代替当地的高程面进行测量计算。反过来说，如果平均高程大于上述相应数据，则不能简单地用大地水准面代替边长的平均高程面。

实际测量时，可先大致估算一下整个测区的平均高程，再根据按现场工程建设精度情况制定的测量技术要求，考虑是否选用大地水准面作为测区基准面。

考虑式（5-2），将其转化为

对于像高速铁路这样的高精密带状线性工程，一般均需考虑此项距离改化。例如，TB 10601—2009《高速铁路工程测量规范》1.0.3条规定，“高速铁路工程测量平面坐标系应采用工程独立坐标系统，在对应的线路轨面设计高程面上坐标系统的投影长度变形值不宜大于10 mm/km”，代入式（5-3）得Hm=63.71 m。在此情况下，如果铁路长10 km，则会产生100 mm的投影长度变形，100 km则会产生1000 mm的变形，以此类推。显然这是不容许的，实际工作中必须建立相应的高程投影面进行距离改化。

如果选择了独立基准面，便须将各条边长投影到独立基准面上。具体的改正计算步骤见本项目任务4。