【摘要】:角度是两条相交直线形成的夹角。测量中的角度是指第一条直线顺时针旋转到第二条直线所转过的量度值。角度既是一个数学概念,又是一个具体的物理量,可以用角度尺测定其大小。图4-1角度的概念图4-2角度尺的应用坐标系中的直线有确定的方向。我们生活中的手表、时钟,它们的时针、分针、秒针均是按顺时针旋转方向为时间增加方向,测量经纬仪中的水平度盘也是按沿顺时针方向读数增加来注记的。
角度是两条相交直线形成的夹角。测量中的角度是指第一条直线顺时针旋转到第二条直线所转过的量度值。如图4-1所示,直线OA与直线OB的夹角为36°,是直线OA绕顶点O顺时针旋转到OB扫过的角度。角度既是一个数学概念,又是一个具体的物理量,可以用角度尺测定其大小(见图4-2)。
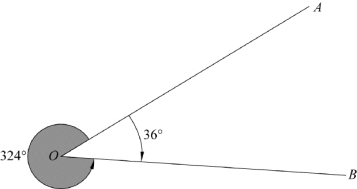
图4-1 角度的概念
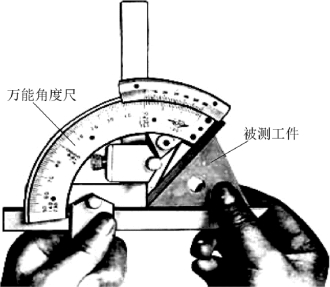
图4-2 角度尺的应用
坐标系中的直线有确定的方向。根据上述定义,我们确定角度也是有方向的。图4-1所示直线OA与直线OB的夹角除了按顺时针方向旋转为36°,还可以是让直线OA沿逆时针方向旋转至直线OB所形成的角度324°。(https://www.xing528.com)
通常情况下,数学坐标系中规定按逆时针方向旋转为正,而测量坐标系中刚好相反(参见图2-11,高斯平面直角坐标系),是按顺时针方向旋转为正。我们生活中的手表、时钟,它们的时针、分针、秒针均是按顺时针旋转方向为时间增加方向,测量经纬仪中的水平度盘也是按沿顺时针方向读数增加来注记的。因此,角度具有顺时针方向和逆时针方向。
所以说,就像力的三要素那样,角度也同样具有大小、方向、作用点这三个基本要素。图4-3显示了在测量坐标系中各条直线之间的夹角关系。直线AB与直线CD相交于O点,直线OC与直线OA的夹角为46°,直线OA与OD的夹角为134°。而直线OD与直线OA的夹角为226°,直线OB与OD夹角为314°。
根据直线延长或缩短时其方向保持不变的性质,我们还可以推断出其他任意两根直线的夹角,例如直线DC与直线OB的夹角便为226°(即直线OC与直线OB的夹角),等等。
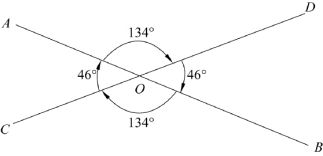
图4-3 直线的夹角
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




