测量基础与实训：直线的方位角与象限角

1.坐标方位角

从标准方向北端起，顺时针方向计算到某一直线的角度，称为该直线的方位角。以真子午线为标准方向的方位角称为真方位角，用A真表示；以磁子午线为标准方向的方位角称为磁方位角，以A磁表示；以坐标纵轴线为标准方向的方位角称为坐标方位角，用α表示。

如图2-22所示，直线P1P2的真方位角A真、坐标方位角α、磁方位角A磁三者之间的关系为

【问题求解】　图2-22中的ε是什么角？

无论是真子午线还是磁子午线，不位于同一条子午线上的各点的子午线方向便互不平行，这使得从直线两端点确定该直线的方向时，计算不方便，所以在日常测量中，广泛采用坐标纵轴的北方向作为标准方向，亦即多采用上述三个方位角中的坐标方位角来进行测量与计算。

图2-23所示为直线OA、OB、OC及OD的坐标方位角α1、α2、α3、α4。

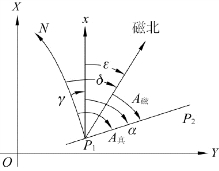
图2-22　三个方位角相互关系示意图

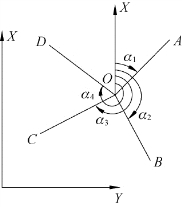
图2-23　坐标方位角

由图2-23可知，坐标方位角是纵坐标轴X按顺时针方向旋转到某一直线所形成的夹角。方位角取值范围为0°～360°，也就是说既没有负值的方位角，也没有大于360°的方位角。当然，如果一定要使用负值的方位角或大于360°的方位角也未尝不可，只是要注意，负值的方位角是逆时针旋转得来的，而且，任何一个负的方位角或正的方位角，加减360°的倍数之后，参与测量坐标计算时，其结果不会受到任何影响。

根据上述方位角的定义及图2-23所示，不难看出，由两个直线方向的坐标方位角可以求得它们之间的夹角。例如，要求∠AOB或∠BOA，则∠AOB=αOB-αOA=α2-α1。同理，有∠BOA=αOA-αOB=α1-α2，若结果是负值，应加360°，即∠BOA=360°+α1-α2。

由此可知，两个方向的夹角等于第二个方向的方位角减去第一个方向的方位角，当不够减（即得负值）时，就应加360°。

2.坐标象限角

测量上有时用象限角来表示直线的方向（如飞机、轮船的航行方向）。象限角就是直线与标准方向线所夹的锐角。如果分别以真子午线、磁子午线和坐标纵线为标准方向，则该象限角相应地称为真象限角、磁象限角和坐标象限角。象限角的取值范围为0°～90°，用R表示。如图2-24所示，直线OA、OB、OC及OD的象限角值分别为R1、R2、R3和R4。

因为同样角值的象限角在四个象限角中都能找到，所以用象限角定向时，除了要知道角值大小之外，还要知道直线所在象限的名称。如图2-24所示中OA、OB、OC和OD的象限角，分别用北R1东（NR1E）、南R2东（SR2E）、南R3西（SR3W）及北R4西（NR4W）表示。例如，假定R1=30°，R2=40°，R3=50°，R4=60°，则分别表示为北30°东，南40°东，南50°西，北60°西。如果指导轮船在大海中航行，则可口述为北偏东30°，南偏东40°，南偏西50°，北偏西60°。

3.坐标象限角与坐标方位角的关系

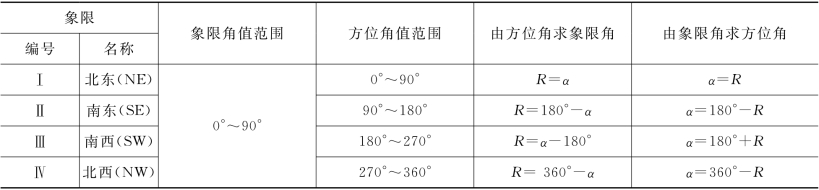
直线的坐标方位角和坐标象限角的关系，如图2-25所示。显然，每条直线的坐标方位角与坐标象限角有一个代数关系，如表2-3所示。

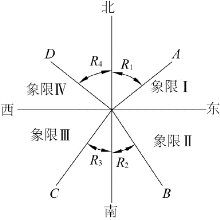
图2-24　象限角

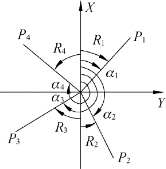
图2-25　方位角与象限角的关系

表2-3　方位角与象限角的换算

(www.xing528.com)

4.直线的正反方位角

一条直线有正、反两个方向。以一个方向为正方向，另一个方向便为反方向，通常取直线前进的方向为正方向。直线的正、反方位角有如下几个特点。

（1）直线的正、反坐标方位角相差180°。

如图2-26所示，如果从A到B为前进方向，则直线AB的坐标方位角用αAB表示，称正方位角；反方向BA的方位角用αBA表示，称反方位角。

图2-26所示的标准方向是坐标纵线，可以看出，由于两端点A、B的坐标纵线方向彼此平行，所以正、反坐标方位角的数值相差180°，即

实际中取正号或负号，以满足0°≤αAB≤360°为原则。

（2）直线的正、反坐标象限角的关系是：角值相等、象限跳跃。即将正象限角中的南、北互换，东、西互换就成了反方向的象限角，如图2-26所示，AB的象限角为北R东，其反方向BA的象限角则为南R西。

（3）直线的正、反真方位角与直线两端点的子午线收敛角有关，直线的正、反磁方位角还与两端点的磁偏角有关。

由于一条任意直线两端点的真子午线互不平行，所以这条直线的正、反真方位角就不是相差180°，还相差这条直线的两端点所在的两个子午线收敛角的差值。参照图2-27，有

从而有

同理可推求得

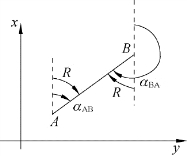
图2-26　正、反方位角与象限角

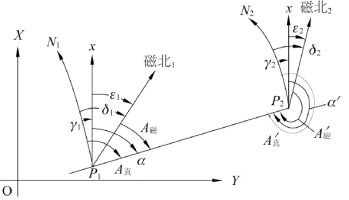
图2-27　直线正、反方位角的关系

可见，一条直线的正反磁方位角相差得更加复杂，除180°之外，不仅相差两端点的子午线收敛角之差，还相差两端点的磁偏角之差。

某点的子午线收敛角、磁偏角又随直线上点位置的不同而不断发生变化，故直线的正、反真方位角（或磁方位角）之间的关系也就不确定。显然，这对于方位角的计算是很不方便也很不切合实际的（计算过程太复杂）。

实际上，一条直线的真方位角或磁方位角不仅与这条直线的方向有关，还与这条直线的方位角起算点位有关，起算点位置不同，则角度大小不同。也可以这样说，一条直线上能找出无数个真方位角或磁方位角，这与坐标方位角完全不同。因此，在一般测量中，通常采用坐标方位角来表示直线的方向。

为方便起见，本书在以后的叙述中，通常将坐标方位角及坐标象限角统称为方位角及象限角。