测量基础与实训：大地高、正高及正常高的概念

在高程系统的概念中，我们经常接触到大地高系统、正高系统、正常高系统这三种高程系统。此外，还有局部地区使用的力高高程系统。

1.大地高系统

大地高是大地坐标（B，L，H）的高程分量H，是指从地面某点沿过此点的法线（与参考椭球面垂直的线）到参考椭球面的距离（图2-15中地面点P与投影点p之间的距离）。由此可见，大地高系统是以参考椭球体面为基准面的高程系统。

大地高又称为椭球高，因为它随着参考椭球体元素的取值不同而不同，所以它只是一个纯数学性的几何量，不具有实质性的物理意义。例如，1954年北京坐标系与1980年西安坐标系的椭球体元素便各不相同，那么同一点在这两种坐标系中的大地高也就不同。全球卫星定位系统GPS测定的高程H便是以WGS-84椭球面为基准的大地高。

2.正高系统

正高系统是以大地水准面为基准面的高程系统，如图2-16所示。正高表示地面点沿铅垂线到大地水准面的距离PO′。而根据本项目任务1的介绍，水准面是处处与铅垂线正交的静止水面（大地水准面则是平均的静止海水面），地面上不同地点的水准面互相之间是不平行的。因此，如图2-16所示，沿不同的水准路线OABCP与OA′B′C′P，进行以水准面为参考依据（仪器整平）的几何水准测量，就算没有任何测量误差（仪器绝对完美，操作绝对精准，外界条件绝对无影响），测量出的P点的高程还是不相同的。这是因为两个相同水准面的不同位置所对应的Δhi与Δhi′并不相等！也就是说，真正的正高高程H=ΔH1+ΔH2+ΔH3+…根本无法精确地测定出来。因为我们不可能从P点钻一条垂直于大地水准面（OO′）的竖井，来测量出该竖井的垂直高度。再说，我们也根本无法找到那个大地水准面（OO′）的位置究竟在哪里（该位置与地球内部结构组织的质量、密度相关）。

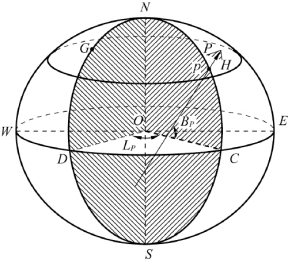
图2-15　大地坐标中的大地高H

图2-16　正高系统的概念

3.正常高系统

因为水准面的不平行性，导致无法测得地面上各点的正高高程。为了解决这一水准测量高程多值性的问题，测绘工作者便要去寻找近似于大地水准面的曲面——似大地水准面，来作为高程测量的基准面。地面点沿过此点的正常重力线到似大地水准面的垂直距离称为正常高。所以说，正常高系统是以似大地水准面为基准面的高程系统，和大地高之间存在高程异常。似大地水准面是从地面各点沿正常重力线量取正常高所得端点构成的封闭曲面。所以说，似大地水准面严格来说不是水准面，但接近于水准面，它是人们用一定方法（重力测量、水准测量）获得的，用于高程计算的辅助面。它与大地水准面不完全吻合，差值为正常高与正高之差。正高与正常高的差值大小，与点位的高程（地表的起伏不平）和地球内部的质量分布息息相关。在我国青藏高原等西部高海拔地区，两者差异可达3～4 m，在中东部平原地区这种差异约为几厘米。在海洋面上时，似大地水准面与大地水准面完全重合。此时，大地水准面的高程基准可同时作为似大地水准面的高程基准使用（如我国的青岛黄海国家高程基准）。

针对地面上某点，其正常高的计算公式可表达为^[2]

式中各项均可精确测量、计算获得。其中，γm为该点正常重力平均值（根据该点的大地纬度B和地心坐标高度计算得到），d h为水准测量的高差（普通几何水准测量方法获得），g为相应水准路线上的重力值（用重力测量方法得到）。所以正常高可以精确测定，其数值可唯一确定，不随水准路线而异。我国幅员辽阔，地形起伏较大，国家规定采用正常高系统作为我国高程控制的统一系统。我国的国家等级水准点高程均为正常高。

另外指出，如果是在大型水库工程建设中，特别是在南北方向上距离较远的工作区域范围内，由于静止水面上不同纬度的点的正高或正常高不相等，但工程设计、施工、放样时又必须要求其相等，为了解决这一问题，便采用力高系统，或采用更加接近本地区正常高的地区力高系统^[3]。

4.三种高程系统的关系

综合上述大地高H、正高H正、正常高H正常的概念与含义，这三种高程系统满足如下关系式：(www.xing528.com)

式中，hm为大地高与正高之差，即参考椭球体面与大地水准面之间的距离，称为大地水准面差距；hm′为大地高与正常高之差，即参考椭球体面与似大地水准面之间的距离，称为高程异常。它们的相互关系可用图2-17表示。

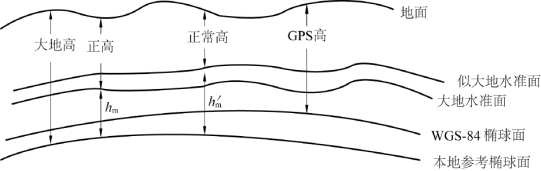
图2-17　三种高程系统的相互关系

正常高的建立与测定主要是用在国家等级的高程测量中。我国的地方高程系统繁多，五花八门。自1985国家高程基准于1988年1月正式启用之后，国家要求各地方尽量采用这一新的国家高程基准（至少进行高程联测）。在一般的工程建设中，由于测区范围相对较小，则范围内的大地高、正高、正常高三者相差的变化不大，此时测量人员仅用几何水准或几何水准结合GPS高程（注意互相印证检查）来进行高程测量，只要能满足相应的工程建设精度要求，也是可取的。对于测区内地形平缓、高差不大的地区，完全可以如此操作。至于一定范围内，大地高、正高、正常高之间的差值到底有多大，如何受测区范围和测区高程、高差的影响，可查阅参考文献［3］第78页有关介绍。

5.国家高程与地方高程的换算

从图2-13中可以看出，高程基准除了用大地水准面外，还可以使用任意水准面作高程基准面。实际工作中我们也会碰到各式各样的高程基准面。图2-18是我国部分地方高程基准与国家高程基准的相互位置示意图。

图2-18中1985国家高程基准面是我国现行的法定高程基准面，其余几种高程基准的数据来自网络百度资料“常用高程基准及换算”等。读者可以根据相关参数（零点差），将本地有关高程系统的基准面插入图2-18中合适位置，以此判断其基准面关于国家高程基准面的相对位置。例如，可以通过网络搜索获得以下资料：

宁波：“1985国家高程基准”注记点=“吴淞高程系统”注记点-1.87。

嘉兴：“1985国家高程基准”注记点=“吴淞高程系统”注记点-1.828（？）。

昆山：“1985国家高程基准”注记点=“吴淞高程系统”注记点-1.662军。

从图2-18中还可以很直观地看出如何进行国家高程与其他高程的换算。

【例2-3】　已知地面某点在1985国家高程基准系统中的高程H国家=30.235 m，求该点的其他高程H珠基、H广州、H黄海。

图2-18　高程系统的相互关系及换算

［解］　珠基高程H珠基=H国家-0.557=29.678 m，广州高程H广州=H珠基+5.000=34.678 m，以及该点在1956年黄海高程系统中的高程H黄海=H国家+0.029=30.264 m。

现在我国规定使用统一的高程基准——1985国家高程基准。那么与此相对应，其他高程基准就变成了假定高程（任意高程、相对高程），例如上海吴淞高程基准、天津大沽高程基准、珠江高程基准、波罗的海高程（新疆部分地区使用）、大连零点高程基准，等等。还有在这些高程基准的基础上衍变出来的高程基准，如吴淞高程系统中的张华浜基点高程、佘山基点高程、镇江308′标点高程，在珠江基准面上添加出来的广州城建高程，等等。如果这些高程基准是根据当地长期的验潮资料确定，并能够以此作为当地的高程基准面进行区域性正常高水准测量，则又可称该高程基准面为假定的似大地水准面。如上海“吴淞高程系统”便是采用上海吴淞口验潮站1871—1900年实测的最低潮位所确定的海平面作为基准面。