在我国现今八种基本比例尺(1∶1 000 000、1∶500 000、1∶250 000、1∶100 000、1∶50 000、1∶25 000、1∶10 000、1∶5 000)地形图中,除了1∶1 000 000小比例尺地形图采用兰勃特正轴等角圆锥投影外,其余各种比例尺地形图均采用高斯横切椭圆柱投影。该投影首先由德国数学家高斯提出和建立,后经克吕格导出严密的投影公式加以补充,故又称为高斯-克吕格投影,简称高斯投影。
1.高斯投影的几何概念
如图2-7所示,高斯投影的几何概念可以叙述如下。
设想一个空心的横椭圆柱体套在参考椭球面上。横椭圆柱体的椭圆与参考椭球体的椭圆完全一致(两椭圆参数相同)。椭圆柱体刚好与椭球面上某一子午线NBS相切(紧密重合),该子午线称为中央子午线,NAS与NCS为边缘子午线并构成一个投影带。A、B、C为三条子午线与赤道的交点,AB、BC弧长相等。此时,椭圆柱体的中心轴OO位于赤道中心平面内,并与椭球体的旋转轴NS相交于椭球体中心I点。假定I点是一个点光源,光线照射使椭球面上的投影带及其图形投影到椭圆柱体面上,然后将椭圆柱面沿过南、北两极的母线L1L2、K1K2剪开,展平,得到NSABC所在的投影平面(见图2-8),该投影平面称为高斯投影平面,简称高斯平面,以此建立的坐标系称为高斯平面坐标系。
2.高斯投影的特点
根据上述投影概念,高斯投影具有如下特点(参阅图2-7、图2-8)。
①中央子午线投影后为直线,长度不变。其余子午线投影后凹向中央子午线,并关于中央子午线对称,离开中央子午线的距离越远长度变形越大。
②赤道投影后为直线。其余纬线投影后凸向赤道,并关于赤道对称。
③经线与纬线投影后,仍然保持互相正交。

图2-7 高斯横切椭圆柱投影
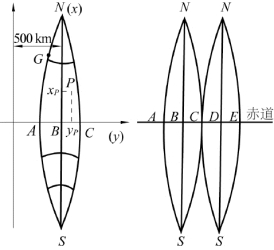
图2-8 高斯投影平面
3.高斯投影带的划分
根据高斯投影的上述第一个特点,距离中央子午线比较远的地方投影长度变形较大,由此引起的面积变形也较显著。为了使长度和面积的变形满足测量制图的要求,投影带必须限制在中央子午线两侧一定范围内。为此,将整个参考椭球体面自本初子午线开始,用子午经线均匀地分成若干等份,每一等份代表一个投影带(见图2-7,第①带,第②带,…)。投影时就类似放幻灯片一样,自东向西慢慢旋转椭球体,将椭球体上各投影带的中央子午线分别与圆柱面紧密重合,依次将各投影带的图形投影到圆柱体面上并剪开,展平,直到将所有投影带投影完成。
如何划分投影带,国际上通行有两种方法,一种是按经度差6°带划分,从本初子午线开始,自西向东每隔6°为一投影带,依次用阿拉伯数字1~60进行编号,全球共分为60个投影带(见图2-9)。另一种是按经差3°带划分,划分时将第1号3°带的中央子午线与第1号6°带的中央子午线重合,然后按每隔3°为一投影带,全球共分为120个投影带。当按6°带划分时,根据地球赤道周长,可以简单计算出沿赤道线位置,每个6°带的两条边界子午线之间最大弧长约为667 km,即每个投影带中距离中央子午线最远处不超过334 km。经投影后此处的线段会产生约1/700长度变形。对于大比例尺测绘地形图,以及要求较高精度的工程测量(测距误差要求1/2000~1/1000)来说,如此大的投影长度变形是不能允许的。因此还要采用3°带,甚至1.5°带来划分,并以此建立高斯平面直角坐标系。
图2-10展示了6°带与3°带的具体划分以及将它们展开之后的相互位置关系。根据图2-10,东半球内的6°带与3°带的带号,与其相应的中央子午线的经度有如下关系:
![]()

图2-9 6°带投影分带
式中,L6为6°带的中央子午线经度;N为6°带的带号;L3为3°带的中央子午线经度;n为3°带的带号。
反之,如果知道某点经度L,则可求算出该点所在6°带带号N或3°带带号n,计算公式如下:
 (https://www.xing528.com)
(https://www.xing528.com)
我国领土范围约为东经73°40′~135°05′。因此,按高斯投影,我国涉及的6°带带号为13~23,共11个投影带,涉及的3°带带号为25~45,共21个投影带,如图2-10所示。
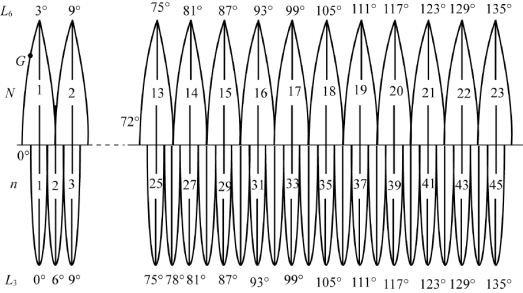
图2-10 6°带与3°带的关系及我国投影带范围
4.高斯平面直角坐标系
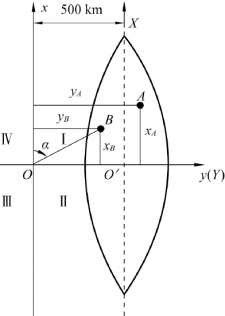
图2-11 高斯平面直角坐标系
图2-8表示参考椭球体面上的经纬线及点P投影到椭圆柱面之上展开成高斯平面、建立坐标系之后的情况。图2-11所示为高斯平面直角坐标系建立情况。投影展开成高斯平面之后,取中央子午线为坐标纵轴,称为X轴;赤道为横轴,称为Y轴;两轴垂直相交于O′点,称为坐标原点,以此建立O′XY平面直角坐标系。该平面直角坐标系便称为高斯-克吕格坐标系,简称高斯坐标系。
该坐标系的纵坐标自赤道向北为正,向南为负;横坐标自中央子午线向东为正,向西为负。我国领土位于北半球,纵坐标X均为正值,表示投影之后坐标点距横轴(Y轴,赤道投影)的距离;横坐标Y则有正有负,其绝对值表示投影点距纵轴(X轴,中央子午线投影)的距离。为了使横坐标也为正值,规定在6°带与3°带中,每带的坐标纵轴往西平移500 km(见图2-11)。平移之后的坐标系为Oxy平面坐标系。坐标系的象限按顺时针方向依次定为Ⅰ、Ⅱ、Ⅲ、Ⅳ象限。
由于高斯投影是按分带法各自进行投影的,故每个6°带或3°带都有自己的坐标轴和坐标原点。根据图2-10,我国6°带投影有11条投影带,3°带投影则有21条。因此,如果仅仅知道某点在自己投影带内的坐标,仍不能确定该点在全国范围内的具体位置。为了明确表示某已知坐标点的具体位置,亦即该已知坐标点属于哪一投影带,规定在每个坐标点的横坐标值前冠上带号。这种加了500 km和带号的坐标系,称为国家统一坐标系,其横坐标用y表示。因此,投影带内任一点的横坐标的统一坐标值y(单位:m)表示为
![]()
式中,Y为以中央子午线投影位置为X轴的横坐标值,称为横坐标的自然值。
因此,国家统一坐标系中的x、y表示的意义为:x表示坐标点在高斯平面上到赤道投影线的距离;y包括投影带的带号、附加值500 000 m和实际平面坐标Y三个参数。
【例2-1】 假设图2-11中A、B两点所在投影带带号为19(我国范围),其高斯平面坐标分别为XA=3 211 567.698 m,YA=131 567.699 m,XB=1 211 567.731 m,YB=-231 567.852 m。试计算该两点的国家统一坐标值。
[解] A点:我国国家统一坐标系与高斯坐标系的纵坐标没有变化(表示坐标点到赤道线的垂直距离),即xA=XA=3 211 567.698 m;横坐标计算根据式(2-3),yA=19带+500 000 m+131 567.699 m=19 631 567.699 m。同样,对于B点有:xB=XB=1 211 567.731 m;yB=19带+500 000 m+(-231 567.852)m=19 268 432.148 m。
【补充说明】 在我国,高斯投影的6°带带号为13~23,3°带带号为25~45,两种投影带没有出现重复的带号,所以根据某点的统一坐标值就可判断出该点的坐标是属于6°带还是3°带(图2-10)。
【例2-2】 已知我国某点M的统一坐标值为x=1511567.138 m,y=38462455.148 m。试分析指出该点所位于的高斯投影带带号、点位,中央子午线经度。
[解] 根据式(2-3),y=带号N(或n)+500 000 m+Y=38 462 455.148 m,带号为38号带,再根据图2-10,38号带属于3°带投影,中央子午线经度为114°。500 000 m+Y=462 455.148 m,可以计算出Y=462 455.148 m-500 000 m=-37 544.852 m。即该点位置位于中央子午线以西,投影后在高斯平面上距中央子午线37 544.852 m,距赤道距离1 511 567.138 m。
5.高斯坐标系与数学坐标系的关系
数学中的直角坐标系是法国数学家笛卡儿在1619年创造的,从此也开创了一门新的数学分支学科——坐标几何(即解析几何)。如图2-12所示,数学坐标系中的横轴是x轴,纵轴为y轴,这与高斯先生两百年之后(1820年)建立的测量坐标系情况刚好相反(见图2-11)。不过,由于各自的方向角均是从x轴起算,方向角旋转的方向分别是按逆时针方向和顺时针方向为旋转的正方向,象限也分别是按逆时针和顺时针设置。因此,数学中的解析几何关系与三角函数公式完全可以适用于测量平面坐标系中。

图2-12 笛卡儿数学坐标系
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




