新RSM方法提升柔性机构动态可靠性

利用二次多项式构造响应面的方法略显僵化,在极限状态方程比较复杂、非线性程度较高的情况下,往往不能有效地逼近真实曲面,影响了响应面的精度。因此,响应面方法在计算精度和计算效率上还有待进一步提高,许多学者在这方面进行了探讨并对传统响应面方法进行了改进,在传统响应面方法基础上得到了很多改进方法,包括单响应面法、多响应面法、序列响应面法、变f序列响应面法、逐步回归响应面法、基于正交多项式的响应面法、基于人工神经网络的响应面法以及基于二水平因子设计的响应面法等。其中,Youn和Choi利用移动最小二乘(Moving Least Square)方法改进了响应面精度^[192];桂劲松和康海贵将ANN方法与RSM方法相结合在结构可靠性分析上取得了良好的效果^[75,193,194];Gomes和Awruch将ANN方法与RSM方法相结合提高了计算速度,并与一次二阶矩方法和MC方法等方法进行了比较^[70];Moore和Sa探讨了多项式响应面设计验算点的最佳选择方法^[195];Gayton和Bourinet探讨了提高RSM计算效率的问题^[196];Guan和Melchers比较了RSM同其他方法的计算效率^[197]。

为了弥补RSM方法处理非线性问题的不足,在不降低RSM方法精度的情况下提高RSM方法的计算速度,将RSM方法的基本原理同ANN技术相结合,本文提出了ANN-RSM方法。该方法的基本原理是用非线性处理能力较强的ANN代替二次多项式构造响应面,其他步骤与传统RSM方法相同。ANN-RSM方法的关键步骤是人工神经网络拓扑结构的设计,本书提出了基于BP神经网络和RBF神经网络的两种ANN-RSM方法。

根据BP神经网络的基本原理,通常情况下采用的BP神经网络为三层拓扑结构。设随机变量为x=(x₁,x₂,…,x_i,…,x_n),按照式(4-65)生成随机变量输入样本,根据输入样本计算系统的动态响应并作为网络的期望输出y=(y₁,y₂,…,y_i,…,y_m)。将输入样本和期望输出样本作为训练样本,给定BP神经网络的训练误差,对神经网络进行训练,采用式(4-23)~式(4-25)进行网络训练,网络收敛后得到神经网络响应面。

另外一种ANN-RSM方法是基于RBF神经网络的响应面方法,RBF神经网络是一种性能良好的前向神经网络,适合于多变量、非线性函数逼近。RBF是一种局部逼近型神经网络,只要隐含层基函数的中心选择得当,仅需少量神经元就能获得很好的逼近效果,可以实现减少计算规模和提高计算速度的目的。RBF神经网络的非线性映射能力由隐含层基函数体现,常见的隐含层基函数有高斯函数、薄板样条函数、多二次函数和逆多二次函数等,本书采用的隐含层基函数是最常用高斯函数^[190],即

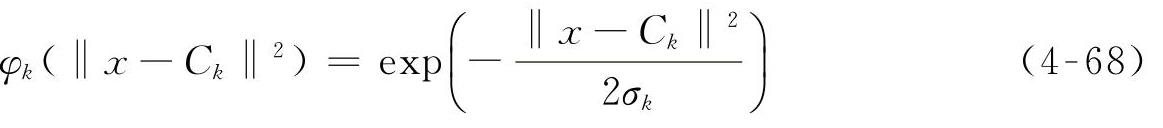
式中 ‖·‖——范数;

C_k——高斯函数中心;

σ_k——高斯函数宽度。

典型的RBF神经网络一般包括输入层(n个神经元)、隐含层(k个神经元)和输出层(m个神经元),如图4-3所示。

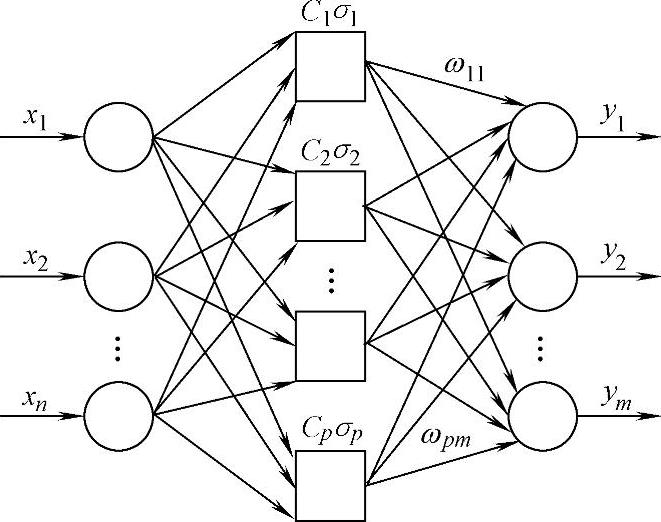
图4-3 RBF神经网络的拓扑结构

图4-3中:

x_i——RBF神经网络的输入样本;

y_j——RBF神经网络的期望输出样本;

ω_kj——连接权值矩阵ω的元素;

C_k——高斯函数中心;

σ_k——高斯函数宽度。

RBF神经网络主要的训练算法有Poggio法、Moddy-Darken法、监督学习法、OLS法和聚类算法等^[190]。RBF网络的学习过程包括隐含层学习和输出层单元学习两个阶段:第一阶段,根据所有的输入样本决定隐含层各神经元的参数C_k和σ_k;第二阶段,按照最小二乘原则,调整输出层权值ω。设输入样本数据为

式中 x_i——第i个随机变量的列矩阵,i=1,…,n;

n——随机变量的数量;

q——第q组随机抽样的样本数据,q=1,…,N;

N——抽样次数。

相应的期望输出数据为

式中 y_j——第j个动态响应;(www.xing528.com)

m——动态响应的数量;

N——对应抽样次数的动态响应次数。

RBF神经网络的某一组输入向量x相对于第k个隐含层节点的输出为

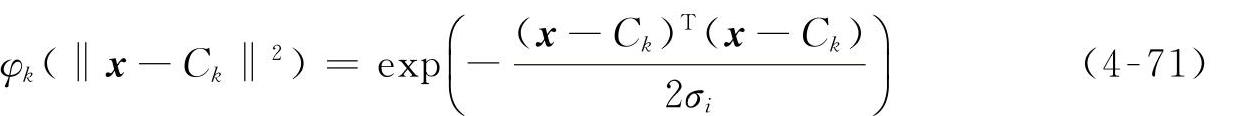
隐含层输出矩阵为

Φ^T=[φ₁φ₂ … φ_p] (4-72)

当输入第q-1组学习样本,神经网络的实际输出y_q-1为

设期望输出y_q-1为

式中 e——误差矩阵。

按照最小二乘原则定义误差目标函数E为

式中 n——随机变量的数量;

e_j——第j组样本的误差;

d_j——高斯函数各个中心间的距离。

第一阶段,根据所有的输入样本确定隐含层各节点的高斯函数的中心C_k和高斯函数宽度σ_k,按照下列方式分别调整输出单元的权值ω_i、隐含层各节点的高斯函数的中心C_k和隐含层高斯函数宽度σ_k。

调整输出单元的权值ω_i:

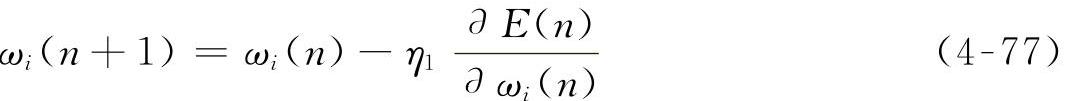
调整隐含层各节点的高斯函数中心C_k:

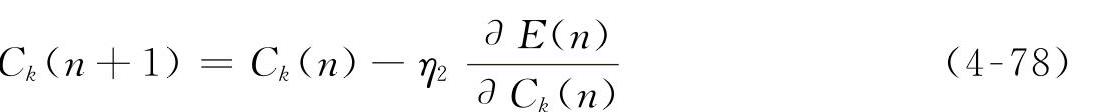
调整隐含层各节点的高斯函数宽度σ_k:

式中 η₁、η₂、η₃——各参数的学习步长。

第二阶段,在确定隐含层的各参数(σ_k、C_k)后,根据样本数据,采用误差纠正算法,如梯度下降法和最小二乘法,调整输出层的权值矩阵ω,直到满足规定的误差精度。