柔性机构动态可靠性分析的RSM方法快速解析

随着机构系统复杂程度的提高,系统随机变量x=[x₁x₂ … x_n]^T的联合概率密度函数f(x)往往未知;同时,机构系统在运动时域内的动态响应与变量输入之间存在着复杂的函数关系,也往往难以获得功能函数g(x)的显式表达式。这类复杂机械系统进行可靠性分析和可靠度计算时,可靠性分析模型不能确定,无法得到功能函数的显式表达式。因此,直接采用FOSM或者AFOSM等方法无法进行可靠性分析和可靠度计算。在这种情况下,用近似方法重构一种显式的功能函数,然后再利用FOSM或者AFOSM方法计算重构功能函数的可靠度指标β(k),用来近似代替未知功能函数的可靠度指标β。其中,RSM方法就是这种重构方法中典型的一种。

RSM方法将复杂系统的可靠性分析问题转化为两个方面:一是利用有限数量的确定性仿真实验重构复杂非线性功能函数g(x);二是高精度地计算设计点x*和可靠度指标β。其中,重构功能函数g(x)是RSM方法的关键,Bucher和Bourgund采用不含交叉项的二次多项式重构功能函数,在均值点和首次拟合获得的验算点之间进行线性插值,将抽样中心近似地选在失效面上^[191];张建国、刘英卫、郑冬青和苏开鑫采用二次多项式重构了弹性机构功能函数的响应面^[119]。通常情况下,利用二次多项式拟合响应面的方法称为传统响应面方法,其基本思想和计算步骤如下:

设x_i(i=1,2,…,n)为可靠度分析中的n个任意分布的独立随机变量,由这些随机变量表示的极限状态方程为g(x_i)=0。响应面方法的基本思想就是构造一个近似的极限状态方程g'(x)来近似替代g(x),即

g(x)≈g'(x)=0 (4-57)

传统构造响应面g'(x)的方法是利用包含交叉项的二次多项式表示响应面函数,待定系数为个,即

式中 x_i、x_j——随机变量;

n——随机变量的数量;

a、b_i、c_i、d_ij——待定系数。

如果要确定式(4-58)方程组的待定系数,需要进行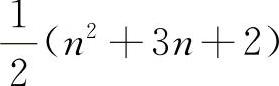组随机变量的抽样计算。考虑到可靠性分析的目的是求解设计验算点和可靠度指标,应用响应面方法在设计验算点附近拟合功能函数时误差较小,而且还可以对响应面函数形式加以简化而不会影响分析结果。同时,当对含有多个随机变量的大型结构进行可靠度分析时,响应面形式的简化将有利于降低可靠度分析的工作量。因此,传统响应面方法中多数采用不包含交叉项的二次多项式表示响应面函数,如果采用不包含交叉项的二次多项式表示响应面函数,则待定系数减少为2n+1个,即

如果要确定式(4-59)方程组的待定系数,需要进行2n+1组随机变量的抽样计算。Bucher提出的响应面算法是在均值点x_μ处形成响应面的,当g_x(x)非线性程度较高,且均值点远离边界时,以均值点为中心点未必能在第一次构成令人满意的响应面;而且一律取随机变量本身的多项式,而不是根据问题的性质以及随机变量本身的特点,也往往不能得到理想的响应面。因此,简单地以均值点x_μ为中心得到的响应面,求得的设计验算点一般情况下不会在极限状态曲面上,因此可靠度指标的精度难以满足要求。对此,Bucher提出了修改随机变量抽样中心点x_M并逐次逼近的方法,在随机变量新的抽样区域内选取的样本点包含了实际极限状态面更多的信息,新的样本中心点x_M选在有均值点x_μ与设计验算点x_D的直线上,并保证在新的中心点x_M处满足g(x_M)=0,即

得到新的中心点后,重新对随机变量进行抽样,求解新的响应面及设计验算点和可靠度指标。

采用如下准则来判定可靠度指标的精度是否满足要求:在新的中心点处响应面的可靠度指标与上次迭代得到的可靠度指标的差小于指定的精度要求,即

式中 ε——设定的可靠度指标的精度;

k——迭代的次数。

当第k次迭代得到的可靠度指标满足精度要求后,可以近似地认为新的设计验算点x_D在极限状态曲面上,即:x^*≈x_D。以新的中心点处得到响应面的可靠度指标β(k)近似代替未知的极限状态方程的可靠度指标β可计算出可靠度R,即(www.xing528.com)

二次多项式响应面方法的计算步骤如下:

1)设初始迭代点为

x⁽¹⁾=(x₁⁽¹⁾,x₂⁽¹⁾,…,x_n⁽¹⁾) (4-63)

随机变量x_i的各个样本点在以下范围内选取:

x∈[x_M-fσ_x,x_M+fσ_x] (4-64)

式中 f——尺度参数,第一次迭代时取f=3.0,第一次迭代之后取f=1.0;

x_M——随机变量抽样样本的中心点,初始迭代时,一般以均值点x_μ为样本中心点,即初始迭代时,各个随机变量样本点的抽样范围是

x⁽¹⁾∈[x_μ-fσ_x,x_μ+fσ_x] (4-65)

2)利用数值方法计算功能函数值。

3)解线性方程组,得到2n+1个待定系数,从而确定二次多项式表示的响应面函数。

4)按照FOSM或者AFOSM方法求解设计验算点x_D^(k)及可靠指标β^(k)。

5)判断|β^(k)-β^(k-1)|是否满足精度要求。如果满足,则输出

如不满足,经线性插值得新的中心点x_M(k)为

以x_M^(k)为中心重新对随机变量进行样本抽样,然后返回2)步进行下一步迭代,直至收敛为止,然后按照式(4-66)输出设计点x^*≈x_D和可靠度指标β=β(k)。