柔性机构动态可靠性分析的FOSM和AFOSM方法

FOSM方法是一种失效模式的功能函数存在显式时的计算方法,基本思路是将功能函数应用泰勒公式在均值点处线性展开,利用基本随机变量的一阶和二阶矩信息,求解可靠度指标,从而得到失效概率^[24]。

设失效模式k的安全裕量方程为

M=g(x) (4-31)

式中 x——随机变量矢量,x=(x₁,x₂,…x_i,…,x_n);

n——随机变量的个数。

设某一失效模式的功能函数g(x)为

g(x)=g(x₁,x₂,…,x_n) (4-32)

将功能函数g(x)在各个随机变量的特定点x^*处按照泰勒公式展开,保留一阶和二阶部分:

如果特定点x^*为随机变量的均值点μ^*,则功能函数的均值和方差为

式中 μ_g——功能函数的均值;

σ_g²——功能函数的方差;

ρ_ij——随机变量x_i和x_j之间的相关系数。

如果随机变量之间相互独立,则

可靠度指标β定义为

则失效概率P_f为

P_f=Φ(-β) (4-38)

FOSM方法依赖于特定展开点的选择,对于同一问题由于所取的极限状态方程不同,求得的可靠度指标β有一定的差别。AFOSM方法是在FOSM方法基础上,为进一步提高精度而改进的方法,与FOSM方法不同之处是:将功能函数按照泰勒公式展开时,并不是在均值点处展开而是在设计点处展开,目的是使可靠度指标β不会由于选择形式不同的等价安全裕量方程而发生变化。

设某一失效模式的功能函数为g(x)=g(x₁,x₂,…,x_n),将随机变量x_i进行正则化处理,即

在n维正则化空间y=(y₁,y₂,…,y_n)中,失效模式的功能函数g(y_i)为

g(y_i)=g(y₁,y₂,…,y_n) (4-40)

相应地,可靠度指标β定义为

从几何上看,β是n维正则化空间中坐标原点到临界破坏面g(y_i)=0最短距离,满足上式的点y^*=(y₁^*,y₂^*,…,y_n^*)为设计点,其对应的随机变量x^*=(x₁^*,x₂^*,…,x_n^*)为

x_i^*=μ_i+y_i^*σ_i (4-42)

设计点y^*就是半径为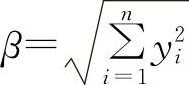的球面与临界破坏面g(y_i)=0的切点,将y^*代入g(y_i)=0,令

g^*(y^*)=g(y₁^*,y₂^*,…,y_n^*) (4-43)

则g^*(y^*)为球面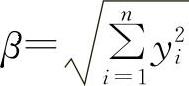和临界破坏面g(y_i)=0在设计点y*处的公共切平面,以两个随机变量(y₁,y₂)的情况为例更加直观地表示,如图4-2所示。图中,坐标(y₁,y₂)分别表示两个随机变量;y^*=(y₁^*,y₂^*)为切点;g^*(y^*)=0为设计点y^*处的公共切平面。

在二维正则化坐标系(y₁,y₂)中,坐标原点O(0,0)到切平面g(y_i)=0的距离Oy*为

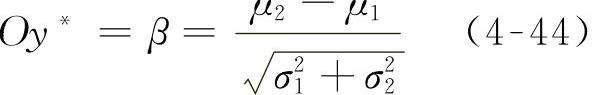
图4-2 可靠度指标β和设计点y^*的几何意义

这种情况可以扩展到有限的n维坐标系中,坐标原点到切平面g(y_i)=0的距离Oy*就是可靠度指标β。对于线性安全裕量方程:(www.xing528.com)

可靠度指标β较容易求出,即

对于非线性安全裕量方程,设计点的求解可以采用拉格朗日乘子法导出公式进行迭代计算。

设拉格朗日函数L为

L=β+λg(y) (4-47)

式中 λ——拉格朗日乘子。

求L的极小值,得

令

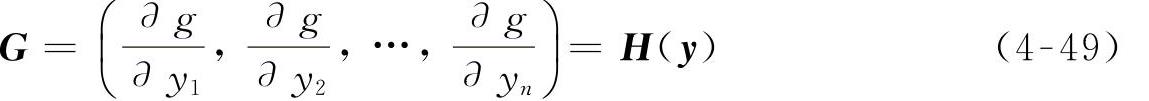
则式(4-48)可以表示为

即

将β所表示的球面写成矩阵形式,有

那么

所以

将式(4-54)代入式(4-51)得

将式(4-55)代入g(y)=0得

g(y)=g^*(β)=0 (4-56)

式(4-56)是关于β的一元方程,可以用数值方法求出β的最小正根。利用AFOSM方法求出β最小正根的迭代实现步骤为

1)设定初始点x^*=(x₁^*,x₂^*,…,x_n^*),定义。

2)形成临界破坏面g(y^*)=0。

3)在y^*处计算和。

4)将y^*=βη_a代入g(y^*)=0并求解,得到β的最小正根。

5)采用第4)步解得的β重新计算y^*=βη_a。

6)重复步骤1)~5),直到计算结果收敛。

7)计算和μ_g=βσ_g。

8)计算x_i^*=μi+σ_iy_i^*。

式中 G^*——设计点处的梯度矢量;

η_a——射线oy^*的方位和角度矢量,表示射线oy^*与各个随机变量y_i坐标轴夹角的方向余弦。