柔性机构动态可靠性分析的MC方法改进成果

许多学者为提高MC方法的抽样效率进行了有益的探索和研究,目前提高MC方法抽样效率的方法主要有期望估计法、重要抽样法和分层抽样法。周则恭等利用重要抽样法改进了MC方法,减少了抽样次数^[187];Papadrakakis和Lagaros利用人工神经网络(Artificial Neural Network,简称ANN)方法与MC方法结合分别求解了静态结构的可靠度和基于可靠度约束的结构优化^[72,188];侯国祥、徐凯、朱梅林等利用ANN方法同MC方法相结合,计算了涡轮增压器压气机叶片的强度可靠性,并与一次二阶矩法、设计验算点法的结果进行了比较^[189]。

为了进一步提高MC方法的抽样效率,使MC方法更加适合柔性机构动态可靠性分析,本文提出了提高抽样效率的ANN-MC方法。该方法利用ANN较强的非线性映射能力,将柔性机构的非线性动态响应随机过程由神经网络模拟实现,即将随机因素影响的柔性机构非线性动态响应复杂的输入输出关系体现在神经网络的输入和输出上。

本文使用ANN方法不仅用于提高MC方法的计算速度,而且降低计算成本,具体实现方法和步骤如下:

(1)确定随机变量样本数据 根据已知随机变量的均值、方差按照MC方法抽取样本数据,将其用于柔性机构动态参数的求解并作为ANN的输入样本。

(2)柔性机构动态参数随机响应的计算 根据MC方法抽取的随机变量样本数据,利用柔性多体系统动力学求解动态参数的随机响应,并将其作为ANN的期望输出样本。

(3)利用样本数据训练ANN 利用ANN非线性映射能力,将随机因素影响的机构非线性动态响应复杂关系由ANN实现,大大减少MC的抽样次数。

(4)进行统计计算 在得到柔性机构动态参数的分布以后,给定设计允许值,即可求出动态参数的可靠度。

ANN具有很强的非线性映射能力,现已证明,适当拓扑结构的ANN可以逼近任何连续非线性函数^[190]。人工神经网络的非线性映射能力由隐含层的映射函数实现,常用的映射函数是神经元的非线性作用函数(Sigmoid函数),例如下式所示的双曲正切函数:

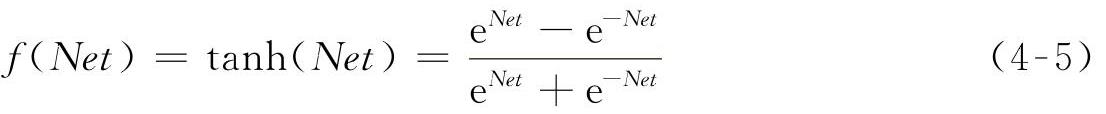
误差反向传播人工神经网络(Back Propagation Network,简称BP)即多层前馈神经网络,是20世纪70年代发展起来的,已经得到广泛的应用。典型的BP神经网络由输入层、隐含层和输出层组成,各层之间单元连接方式为全相连,每层之间单元互不连接,如图4-1所示。

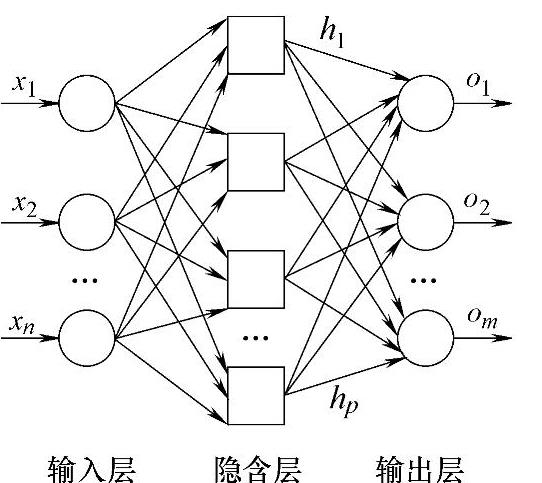
图4-1 BP神经网络的拓扑结构

图4-1中 n——输入层神经元数量;

p——隐含层神经元数量;

m——输出层神经元数量;

x_i——神经网络输入,i=1,…,n;

h_k——隐含层输出,k=1,…,p;

o_j——神经网络期望输出,j=1,…,m。

设ω_ik为输入层的第i个神经元输入到隐含层的第k个神经元的连接强度(权值),即:输入样本矩阵X=[x₁,x₂,…,x_i,…,x_n]^T的第i个分量以权值ω_ik输入到隐含层的第k个神经元中,网络中所有的输入层到隐含层的权值ω_ik构成权值矩阵ω,即

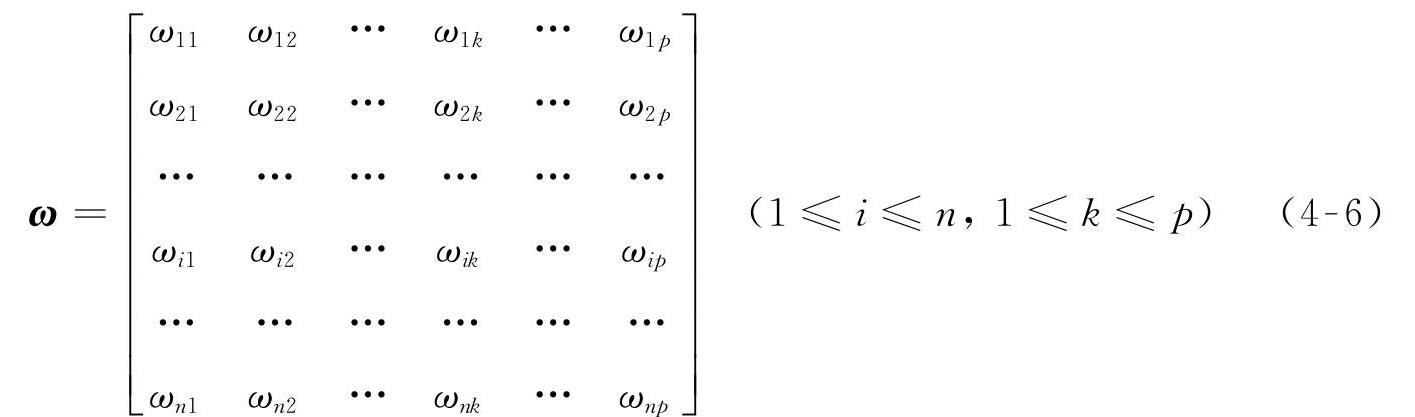
人工神经网络通过提供的样本数据进行学习训练,即:将样本数据集合以样本矩阵形式输入到人工神经网络,作为输入层的激活值,隐含层各个神经元的输入Net_k为

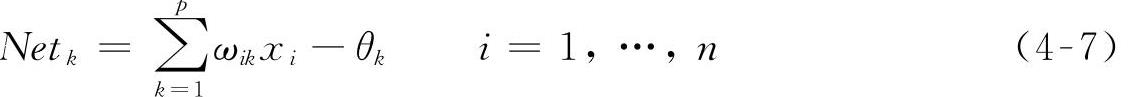
式中 θ_k——隐含层第k个神经元的阈值。

式(4-7)也可以表达为矩阵形式,即(www.xing528.com)

Net=ωX-θ (4-8)

式中 Net——隐含层各个神经元的输入矩阵;

ω——输入层到隐含层的权值矩阵;

X——样本矩阵;

θ——隐含层阈值矩阵。

隐含层各个神经元的输出h_k为

h_k=f(Net_k) k=1,…,p (4-9)

设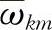为隐含层的第k个神经元输入到输出层的第m个神经元的连接强度(权值),网络中所有的隐含层到输出层的权值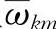构成权值矩阵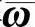,即

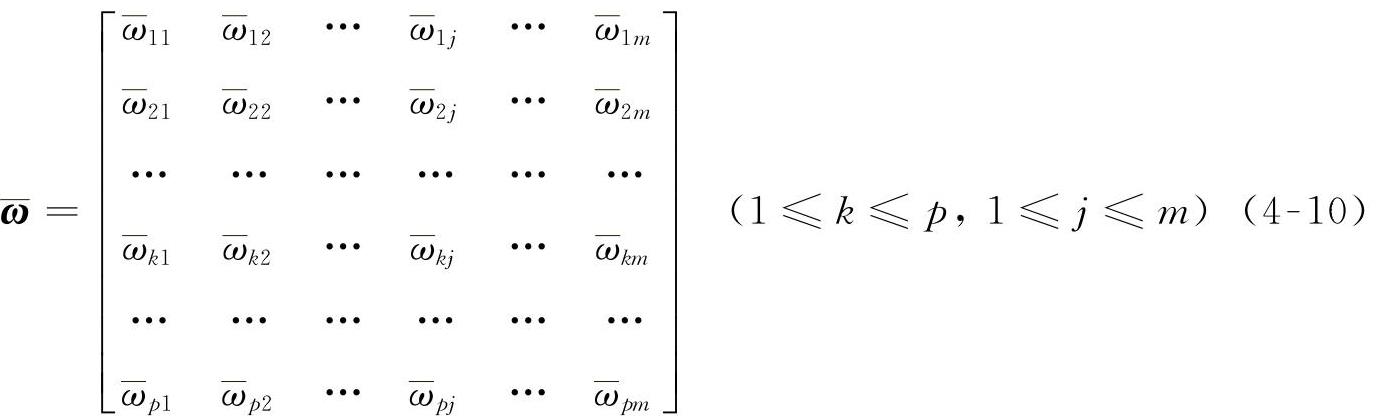
样本数据经输出层各个单元传播后,在输出层的神经元得到人工神经网络的响应,神经网络的输出o_j为隐含层各个神经元输出h_k的线性组合,即

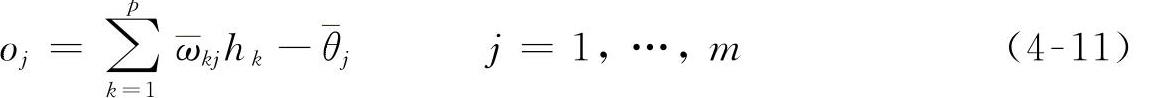
式中 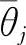——输出层第j个神经元的阈值。

式(4-11)也可以表达为矩阵形式,即

式中 O——输出层各个神经元的输出矩阵,即神经网络的输出响应;

——隐含层到输出层的权值矩阵;

h——隐含层输出矩阵;

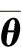——输出层阈值矩阵。

神经网络的实际输出值O和期望输出值Y=[y_j]^T的误差E为

将误差信号从输出端反向传播,并在传播的过程中对权值进行修改,使输出层的神经元的实际输出O和期望输出Y的误差满足给定的学习精度要求。

如果样本数据X共有N组,完成每组样本训练以后均调整网络的权值,然后送入下一组样本数据进行类似的训练,直到完成N组样本的训练学习为止。人工神经网络从样本数据中汲取的知识,就以权值矩阵的形式存储起来。人工神经网络具有泛化能力,当已经训练好(即学习精度达到要求)的人工神经网络遇到未知问题时,可以通过训练的知识积累得到相应的解答。