MC方法的基本原理及柔性机构动态可靠性分析

MC方法的理论基础来自概率论中的两个基本定理,根据柯尔莫哥洛夫大数定理:设x₁,x₂,…,x_n是n个独立的随机变量,若他们来自同一母体,有相同的分布,且具有有限的期望值_μ和方差σ²,则对于任意ε＞0有

即:当n足够大时,随机变量的平均值将收敛于期望值_μ。

根据贝努利原理:若随机事件A发生的概率为P(A),在N次独立试验中,事件A发生的频数为N_A,频率为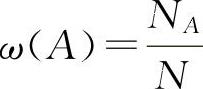,则对于任意ε＞0有

即:当N足够大时,频率以概率为1收敛于P(A)。

如果随机变量x=(x₁,x₂,…,x_n)的联合概率密度为f(x),则失效概率P_f为(www.xing528.com)

式中,D为失效域。如果随机模拟样本点的总数为N,落入D的样本点数量为N_f,将N_f与N的比值作为失效概率P_f的无偏估计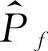,则

MC方法无需知道分布类型及概率参数,适用于各种分布的抽样统计,对于解析法难以处理的分布,用模拟法来求解更显出其优点。随着模拟次数的增加,模拟结果的精度也随之提高。但是,由式(4-4)可知,当失效概率P_f非常小时,需要模拟很多次才可能出现1次失效事件。在失效概率非常小的情况下,由于所需的模拟次数N太大,模拟计算的时间成本较高。

柔性机构系统为动态随机系统,利用直接抽样的MC方法求解柔性机构动态可靠性时,需要从t₀=0时刻开始,在整个运动时域T内对柔性机构的随机过程进行模拟。通常情况下,求解DAEs形式的柔性机构动力学方程所需要的时间步长Δt很小,一次抽样仿真的计算量已很可观,又由于柔性机构的高可靠性要求,失效概率P_f很小,导致直接抽样的MC方法计算成本很高,有时甚至无法承受时间的消耗。因此,需要对MC方法进行改进,提高MC方法的效率。