柔性机构随机过程描述及动态可靠性分析

假设随机试验的样本空间为S={e},如果对于每个e∈S,对应有参数t的函数X(e,t),t∈T⊂(-∞,+∞),那么,对于所有的e∈S,得到一簇t的函数:

{X(e,t),t∈T} (2-77)

将X(e,t)称为随机过程,简记为:{X(t),t∈T}或者X(t)。

图2-4 随机过程示意图

对于S中的每一个特定的e,X(t)是仅依赖于t的函数,称为随机过程的样本函数,用x(t)表示,样本函数是随机过程的一次物理实现或一次仿真实现。对于T中每一个特定的t_j,X(t_j)是一个随机变量,称为随机过程在t=t_j时刻的状态变量,简称状态。如图2-4所示,x_i(t)(i=1,2,…,n)为随机过程X(t)的样本函数。对于多次物理实现或多次仿真得到的所有t_j∈T的状态,随机过程在t_j时刻的状态X(t_j)是一簇随机变量。

随机过程可能取值的集合称为状态空间S,其中的每个元素称为一个状态,是X(t_j)以某一概率的取值。参数t的集合为非空集合,随机过程{X(e,t),t∈T}为随机函数。

图2-4中:x_i(t)为随机过程的一次物理实现或者仿真实现,i=1,2,…,n,t∈T;X(t_j)={x₁(t_j),x₂(t_j),…,x_n(t_j)}为特定时刻t_j∈T的一簇随机变量。

对于随机过程X(t)参数集T中的任意n个元素:t₁,t₂,…,t_n,随机过程存在n个状态:X(t₁),X(t₂),…,X(t_n),其联合分布函数为

F(x₁,x₂,…,x_n;t₁,t₂,…,tn)=P{X(t₁)≤x₁,X(t₂)≤x₂,…,X(t_n)≤x_n} (2-78)

式(2-78)为随机过程X(t)的n维分布函数,如果存在非负函数

f(x_i;t_i)=f(x₁,x₂,…,x_n;t₁,t₂,…,t_n) (2-79)

使得

成立,则称f(x₁,x₂,…,x_n;t₁,t₂,…,t_n)为随机过程X(t)的n维概率密度。一般情况下,分布函数族

{F(x₁,x₂,…,xn;t₁,t₂,…,t_n),n=1,2,3,…}(2-81)

或者概率密度族

{f(x₁,x₂,…,x_n;t₁,t₂,…,t_n),n=1,2,3,…}(2-82)

能够完全地确定随机过程的统计特性。特别地,如果对于任何正整数n,随机过程的任意n个状态都是相互独立的,则随机过程为独立随机过程,这时有

设X(t)为随机过程,如果对于任意给定的t∈T,E[X(t)]存在,则将随机过程X(t)的数学期望为

μ_X(t)=E[X(t)] (2-85)

称μ_X(t)为随机过程X(t)的均值函数。对于任何t∈T,μ_X(t)是t的函数,为随机过程X(t)的所有样本函数在t处函数值的加权平均,如图2-5所示(粗实线)。

随机过程X(t)的二阶中心矩为

σ²_X(t)=D[X(t)]=E{[X(t)-μ_X(t)]²} (2-86)

σ_X²(t)称为随机过程X(t)的方差函数,σ_X(t)称为随机过程X(t)的均方差函数,描述随机过程X(t)的所有样本函数在t处函数值相对于μ_X(t)的偏离程度,如图2-5所示(虚线)。

图2-5 随机过程的均值与方差

图2-5中:x_i(t)表示第i次物理实现或者仿真实现过程;μ_X(t)表示随机过程的均值函数;σ_X(t)表示随机过程的方差函数。特别地,随机过程X(t)在时刻t_j为随机变量,均值为μ_X(t_j),方差为σ_X(t_j)。对于随机过程X(t)在任意t1∈T、t2∈T的两个状态X(t₁)、X(t₂),它们的二阶原点混合矩为

ρ_X(t₁,t₂)称为随机过程X(t)的相关函数。其中,f(x₁,x₂;t₁,t₂)是随机过程X(t)在t₁、t₂处的二维概率密度。两个状态X(t₁)、X(t₂)的二阶原点混合矩为

γ_X(t₁,t₂)=E{[X(t₁)-μ_X(t₁)][X(t₂)-μ_X(t₂)]} (2-88)

γ_X(t₁,t₂)称为随机过程X(t)的协方差函数。ρX(t₁,t₂)、γ_X(t₁,t₂)描述的是随机过程X(t)任意两个不同状态的统计特性。

柔性机构运动时域T内的随机过程包括以下几种。其中,前三种为参数的随机过程;后两种为动态响应的随机过程。

(1)随机参数 指构件或者约束的材料、物理和几何等参数,这些参数的随机性源于制造过程的差异,但是在柔性机构运动时域内的一次物理实现或者仿真实现中为确定性参数,可以看作是均值函数、方差函数以及状态变量均为常值的随机过程。

(2)输入参数的随机过程 输入参数是指柔性机构的驱动力、驱动力矩、摩擦因数阻尼力和阻尼力矩等参数,在运动时域中考虑为平稳随机过程。特别地,在均值函数和方差函数为常值的特定时域内可以看作严平稳随机过程。

(3)安全域和失效域的随机过程 安全域是指运动时域内任意时刻的许用域,在运动时域内随时间的变化通常为平稳随机过程,失效域是安全域在状态空间的补集。具有确定性边界的安全域和失效域可以看作是均值函数为常量、方差函数为0的随机过程特例。

(4)拓扑结构参数的随机过程 拓扑结构参数是指构件之间或者构件与约束之间的位形参数,例如构件之间以及构件和约束之间的相对位置、角度等。拓扑结构参数在运动时域内的动态响应过程通常情况下为复杂的非平稳随机过程。

(5)动力学参数和运动学参数动态响应的随机过程 动力学参数(例如机构传递的力和力矩等)和运动学参数(例如位移、角位移、速度、角速度、加速度和角加速度等)的动态响应过程通常情况下为复杂的非平稳随机过程。

在柔性机构特定的运动时域内,输入参数的均值函数和方差函数不随时间的改变而发生变化,这种随机过程X(t)为严平稳随机过程。例如柔性机构在恒定驱动时,摩擦因数、驱动力、驱动力矩、阻尼力和阻尼力矩的随机过程为严平稳随机过程,如图2-6所示。

图2-6中曲面表示柔性机构输入参数在一次物理实现或者仿真实现中的分布函数,曲线表示状态变量对应的分布曲线,其中:t轴表示时间;x轴表示输入参数;f轴表示输入参数的分布函数;μX表示输入参数的均值。对于运动时域内任意时刻t∈T,输入参数的变化如果是严平稳随机过程,其联合分布函数为

(www.xing528.com)

图2-6 柔性机构的严平稳随机过程

F(x₁,x₂,…,x_n;t₁,t₂,…,t_n)=F(x₁,x₂,…,x_n;t₁+ε,t₂+ε,…,t_n+ε) (2-89)

式中,ε为任意实数,满足(t_i+ε)∈T,(i=1,2,…,n)。

严平稳随机过程的均值函数μ_X(t)和方差函数σ_X²(t)为常量,即

μ_X(t)=μ_X,t∈T (2-90)

σ_X²(t)=σ_X²,t∈T (2-91)

对于每次物理实现或者仿真实现的任意时刻t∈T,柔性机构的严平稳随机过程参数分布均为(μ_X,σ_x²,)。随机过程任意时刻t∈T的A-A切面如图2-7所示。图2-7中,X(t)表示随机过程任意时刻t∈T输入参数的状态变量。

柔性机构输入参数在一次物理实现或者仿真实现中各个时刻的取值(样本)可以由运动时域内随机过程的n个状态变量X(t₁),X(t₂),…,X(t_n)来表示,如图2-8所示。

图2-8中曲线表示输入参数在一次物理实现或者仿真实现中各个时刻的取值,任意时刻t_i的状态变量为X(t_i),表示输入参数在时刻t_i的取值。

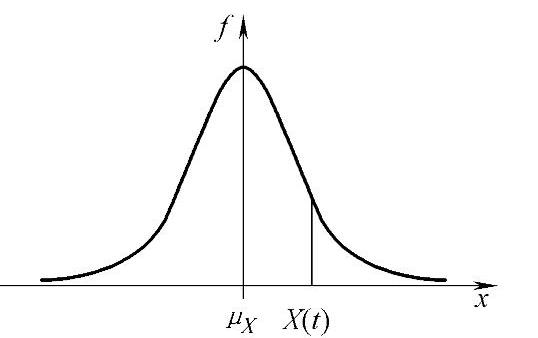
图2-7 严平稳随机过程任意时刻t的分布(A-A切面)

柔性机构的安全域和失效域在运动时域内是时变的,这种时变特性体现在安全域和失效域边界的变化上,即边界的均值函数Ω(t)和方差函数σ_Ω²(t)是时间的函数。当σ_Ω²(t)为0时,边界为确定性边界;当σ_Ω²(t)非0时,边界为随机性边界。如果柔性机构安全域和失效域的边界是随机的,那么安全域和失效域的变化过程也可以看作随机过程。例如:由于环境因素、疲劳的影响,材料的强度极限随时间的增加而下降,强度极限的这种变化为随机过程。因此,在进行可靠性分析时,具有随机性边界的安全域和失效域应考虑为随机过程。而具有单侧或者双侧确定性边界的安全域和失效域,可以看

图2-8 柔性机构参数的严平稳随机过程

作任意时刻的分布函数均为均匀分布的随机过程,如图2-9所示。

图2-9中,曲面表示柔性机构在运动时域内的安全域,曲线表示动态响应对应的分布曲线。具有确定性边界的安全域在任意时刻的分布函数如图2-10所示。

图2-9 具有确定性边界的安全域

图2-10中,X(t)表示t时刻的动态响应;Ω(t)表示t时刻的安全域。

当柔性机构的动态响应在t时刻满足X(t)∈Ω(t)时,则认为柔性机构满足可靠性要求,反之则认为失效。由此推广到整个运动时域,当柔性机构任意时刻的动态响应均在安全域内时,则认为柔性机构满足可靠性要求。在运动时域内的任意时刻,动态响应的取值如果不在安全域内,则认为柔性机构不满足可靠性要求,如图2-11所示。

图2-10 具有确定性边界的安全域

图2-11中,曲线表示在一次物理实现和仿真实现中各个时刻动态响应的取值。在运动时域内均位于安全域内,表示动态响应处于安全可靠的状态。当动态响应在运动时域内向上或者向下跨越边界时,表示动态响应处于失效状态。

柔性机构动态响应主要包括柔性机构的拓扑结构参数、动力学参数和运动学参数的响应,在运动时域内是复杂的随机过程,这些动态响应的均值和方差为时变函数,如图2-12所示。

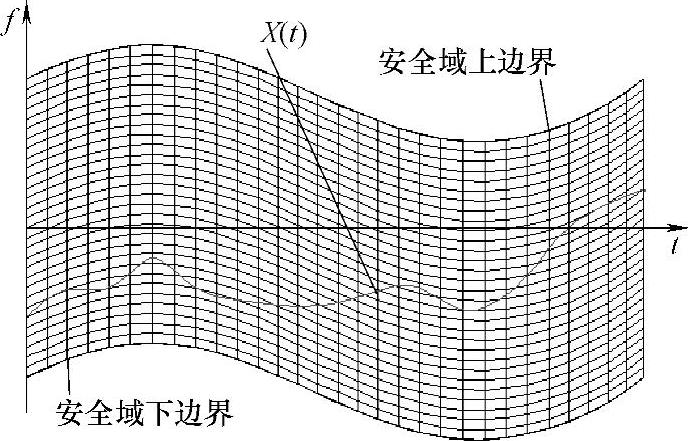
图2-11 柔性机构动态参数的随机过程

图2-12 柔性机构动态参数的非平稳随机过程

图2-12中曲面表示柔性机构动态响应在一次物理实现或者仿真实现中的分布函数,曲线表示动态响应对应的分布曲线,各个变量符号的含义同上。

进行动态响应分析时,通常情况下有两种考察方式:一种情况是考察运动时域内各个运动周期(或者每次仿真)中最大动态应力、最大变形、最大速度等运动参数极值的动态响应;另一种情况是考察特定时刻或者特定时段的动态响应。

极值的动态响应为随机变量,存在两种随机性:其一是极值的出现时间不确定,其二是极值的大小不确定。这种随机性既体现在具有多个运动周期的柔性机构不同运动周期中,也体现在同一种柔性机构不同的仿真实现中。动态响应的极值在运动时域各个运动周期中往往是离散分布的,需要在整个时域内进行分析。

特定时刻的动态响应为随机变量,主要考察动态响应的均值函数和方差函数在特定时刻的分布规律,即考察动态响应随机过程时间截口随机变量的分布规律,在柔性机构运动参数和运动精度可靠性分析、动力参数和动力精度可靠性分析中得到广泛应用。非平稳随机过程动态响应的分布特性如图2-13所示。

图2-13 柔性机构动态参数的非平稳随机过程

图2-13中:

1)图2-13a中曲面表示动态响应的分布函数。

2)图2-13b中曲线分别表示t₀时刻、t_i时刻和t_n时刻动态响应的分布函数。

求解动态响应的时域分布规律是柔性机构动态可靠性分析的关键,但是由于这项研究的难度和复杂程度很高,动态响应随机过程的分布规律无法得到精确解答,只有不同精度的近似方法。动态响应在各个时刻的状态变量如图2-14所示。

图2-14中曲线表示动态响应在一次物理实现或者仿真实现中各个时刻的取值,任意时刻t_i的状态变量为X(t_i),表示动态响应在时刻t_i的取值。

图2-14 柔性机构动态响应的非平稳随机过程