柔性机构动态可靠性分析：随机分析方法

随机柔性机构在运动时域T内的运动过程是一个随机过程,包括随机拓扑结构的时间变化过程、随机动态响应的变化过程以及安全域随机边界的变化过程。将运动时域内随机柔性机构按照一定时间间隔离散为若干个随机拓扑结构,在每个离散的随机拓扑结构中,按照随机结构分析方法进行分析。相应地,随机动态响应和安全域随机边界的变化过程也按照时间截口进行离散。在每个单位时间段中,假设柔性机构的拓扑变化和耦合运动引起的机构动态响应是平稳的随机过程,运动过程则转换为单位时间段随机过程的组合。通过单位时间段动态响应的分布对运动过程的动态参数分布进行参数估计。

随机模拟方法是动态系统可靠性仿真的一种方法,是通过对随机变量的数字模拟和统计分析求取数学物理、工程技术问题近似解的数值方法^[148,149]。蒙特卡罗法(Monte Carlo,简称MC)是一种主要的随机模拟方法,并衍生出多种旨在提高运算速度和计算精度的算法。MC方法求解问题主要有以下步骤:

1)随机变量的抽样。

2)样本反应求解。

3)计算反应量的统计量估计。

MC方法被广泛应用于非线性系统的随机模拟以及复杂结构和机构的可靠性仿真研究,MC方法是公认的相对精确的方法,常用来检验其他近似方法的精度,尤其是新提出的一些近似方法的精度。但是该方法的计算效率较低,为了得到较高的精确度需要很大的计算开销。

柔性机构的随机模拟方法原理是:确定柔性机构系统的随机变量,按照MC方法对随机变量进行随机抽样,根据柔性机构确定性运动学方程进行动力学和运动学分析,获得随机动态响应样本数据,根据随机动态响应样本数据的分布和柔性机构动态可靠性要求确定柔性机构动态可靠度。

另外,摄动方法也是一种随机分析方法,确定性摄动方法与随机性摄动方法的区别有以下几点:确定性参数摄动理论建立在渐近序列的概念上,而随机性参数摄动不存在这一概念;随机性参数摄动以解答的数字特征收敛为标准,因此有所谓M阶精度的概念,而确定性参数摄动则没有这一概念;确定性参数摄动理论研究的主体是奇异摄动理论,而随机性参数摄动理论研究则尚限于具有M阶精度的正则摄动问题^[150-152]。

在确定性结构分析的摄动方法中,控制方程为含有小参数的方程,即

L(u,x,ε)=0 (2-46)

式中 L——一般线性算子;

u——物理问题的解,u=u(x,ε);

x——自变量;

ε——一个小变量。

一般情况下,上述问题往往不能精确地解出,可以用关于ε的一个渐近展开式表示u,如

u(x,ε)=u₀(x)+εu₁(x)+ε²u₂(x)+…+εⁿu_n(x)+… (2-47)

式中,系数u_i(x)与ε无关,将其代入控制方程可以得到

(L₀u₀-h)+(L₀u₁+L₁u₀)ε+(L₀u₂+L₁u₁+L₂u₀)ε²+…=0 (2-48)

式中,L₀、L₁、L₂为线性算子,h为关于x的实函数,可以根据具体问题确定其形式。

对于随机性结构,摄动分析转化为含有随机参数的微分方程,即

L(y,x,ζ)=0 (2-49)

式中,ζ为某个给定分布的随机变量,y=y(x,ζ)为一随机函数。将随机变量转化为标准随机变量表示的形式,有

ζ=ζ₀+ζ_rb=ψ(b) (2-50)

式中,ζ₀为ζ的均值,ζ_b为ζ的均方差,b为均值等于0、方差等于1的标准化随机变量。随机函数y=y(x,ζ)可以展开为关于b的级数,即

上式也可以等价地写成

y(x,ζ)=u₀(x)+bu₁(x)+b²u₂(x)+… (2-52)

其中,系数u_i(x)与b无关,为一确定性函数。代入控制方程可得

(L₀u₀-h)+(L₀u₁+L₁u₀)b+(L₀u₂+L₁u₁+L₂u₀)b²+…=0 (2-53)

式中,L₀、L₁、L₂为线性算子,h为关于x的实函数,可以根据具体问题确定其形式。上式成立的充分条件是各项系数为0。由此可以得到

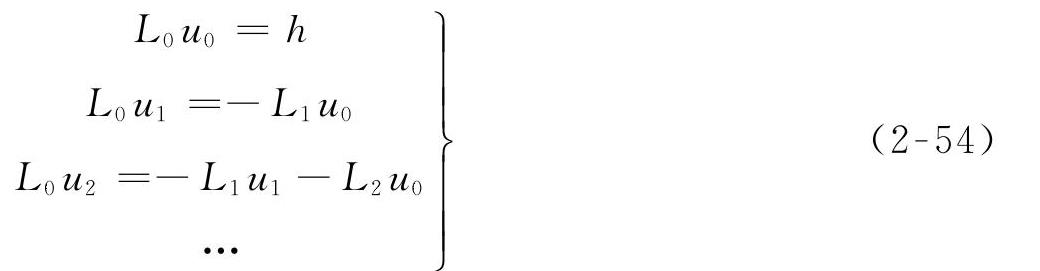
上述方程为确定性方程,当给定边界条件或者初始条件时,可以依次求出u₀、u₁、u₂、…,代入控制方程即可以求出y=y(x,ζ),其均值和方差分别为

E[y(x,ζ)]=u₀(x)+u₂(x)+… (2-55)

D[y(x,ζ)]=u²₁(x)+u²₂(x)+… (2-56)

此外,正交展开方法也是一种随机分析方法,在20世纪90年代逐渐发展起来,成为目前进行随机结构动力分析的主要方法。同摄动方法和随机模拟方法相比,正交展开理论在运算速度和计算精度上都具有很大的优越性。该方法的主要思想是:在随机响应空间中选择适当的正交基函数,将含有随机参数的随机结构动力方程进行次序正交分解,导出随机结构动力系统的扩阶方程,并在复合概率测度空间中进行扩展,建立复合随机振动的扩阶系统方法^[153-157]。

对于随机向量b=(b₁,b₂,b₃,…,b_n),各个分量之间相互独立,在随机函数空间的概率测度定义为

式中,Ω_u为关于u的给定集合,且

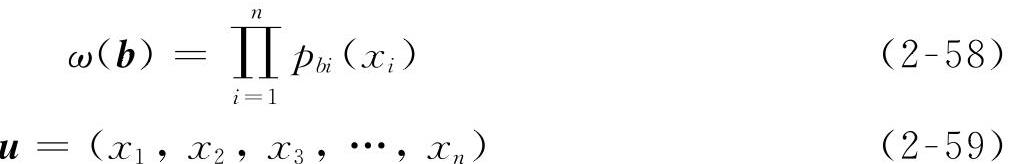
p_bi(x_i)为关于b_i的概率密度函数。若存在基函数系{H_l(b),l=0,1,2,…},且满足

式中,Ω_b为关于u的定义域。对于任意函数Y(b)可以展开为如下形式:

Y(b)=x_lH_l(b) (2-61)

式中,,则称随机函数Y(b)为关于随机变量集合函数的正交展开。(www.xing528.com)

对于随机柔性机构系统动力学方程,利用正交分解可以转化为以下形式:

式中,N_m、N_c、N_k分别为质量矩阵、阻尼矩阵、刚度矩阵中所考虑的独立随机变量的个数。

通过次序正交分解,利用扩阶方法对上式进行改造,可以导出如下扩阶系统方程:

按照参考文献[48]提供的分析方法,将位移x的动态响应展开并进行三阶截断,可以得到随机柔性机构动力学方程的离散形式的代数方程为

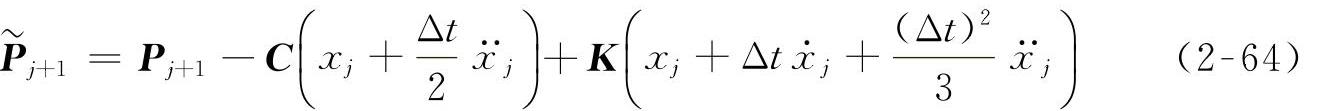
对于含有随机参数的柔性机构的动力响应分析,可以将柔性机构的动力学方程简化为

这是一个多自由度系统的动力学微分方程的一般形式,式中,M为质量矩阵;C为阻尼矩阵;K为刚度矩阵,为n×n实对称矩阵;x(t)为系统的动态响应;F(t)为系统的激励,为n维列阵。

根据摄动思想,可将随机柔性机构动力学方程写成

式中,F(t)为确定性时间过程,根据随机参数摄动分析的基本思想,将随机加速度、速度、位移的响应展开为基本随机变量ζ的级数,即

将式(2-67)代入式(2-68),得到随机柔性机构动态响应分析的递推方程组为

则位移响应的均值为

E[Y(t)]=X₀₀₀…0(t) (2-69)

位移响应任意两个时间点的相关函数矩阵为

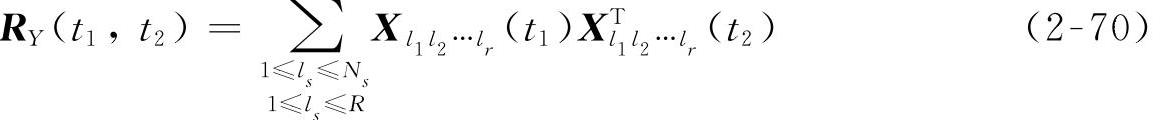
任意两个时间点之间的协方差为

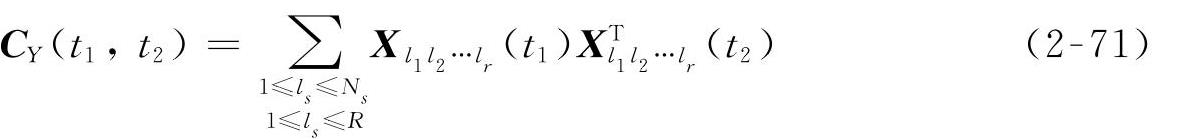
在t=t₁=t₂时,协方差矩阵退化为方差矩阵,即

位移方差向量为

相应地,也可以求出速度、加速度响应的均值和方差。

模糊分析方法也可以应用到可靠性分析中,在常规随机柔性机构模型中,动态性能和动态强度等功能通常以极限状态来描述,当处于极限状态时,柔性机构则处于安全和失效的临界状态,即:柔性机构从安全状态到失效状态是以突变的形式发生的。

柔性机构在随机因素影响下的动态响应为强非线性,动态参数在运动时域中会产生一定程度的“波动”,当这种动态参数的“波动”发生在允许值附近时,简单地认为“凡是超越极限状态就是失效”的观点缺乏说服力,有失科学性,也不符合工程实际。一方面在确定柔性机构动态性能和动态强度可靠性要求时依赖人们的主观判断,具有主观模糊性;另一方面柔性机构动态响应的波动性也具有客观模糊性。为了描述柔性机构的这种状态模糊性,按照模糊理论和方法定义了柔性机构的模糊状态。

柔性机构考虑状态模糊的情况,是指从安全状态过渡到失效状态不是突变的,而是存在一种从安全状态到失效状态的过渡状态,通常情况下,这种模糊状态由动态响应的隶属度函数μ_X(t)来确定。最常见的模糊分布隶属度函数为正态型^[60],如图2-3所示。

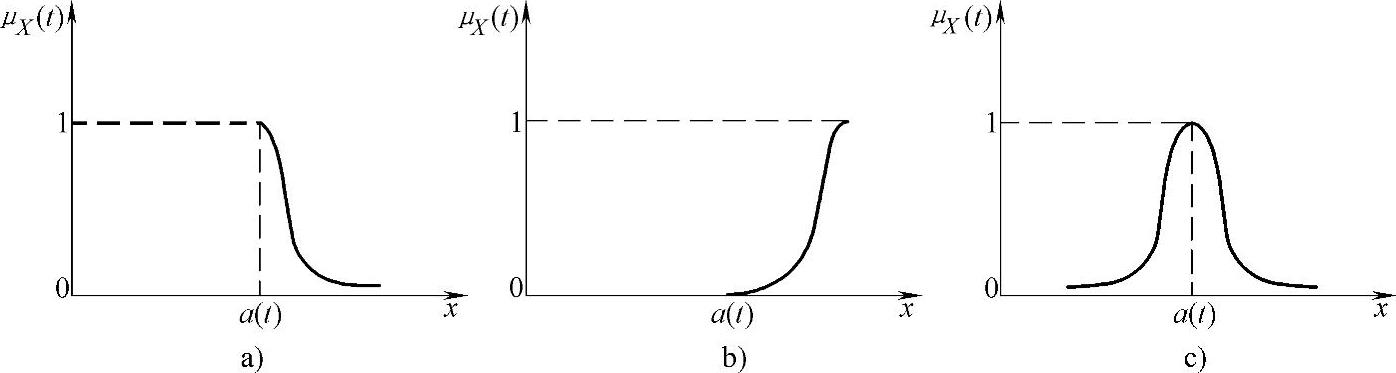
图2-3 隶属度函数

a)偏小型 b)偏大型 c)中间型

(1)偏小型(见图2-3a)

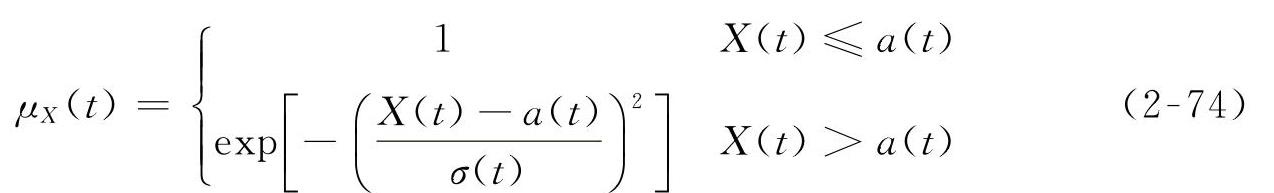
(2)偏大型(见图2-3b)

(3)中间型(见图2-3c)

式中 a(t)——在时刻t动态响应的模糊界限;

σ(t)——在时刻t动态响应的模糊分布参数。

通过上述模糊隶属度函数μ_X(t),可以描述动态响应在运动时域内任意时刻t的模糊状态。