柔性机构动态可靠性研究

包含柔性构件的机构系统实质上是一个柔性多体系统,是一个包括柔性构件、刚性构件以及运动副的动态系统。柔性机构系统的确定性模型主要包括柔性机构的物理参数、外力参数、拓扑结构、约束方式和运动时域等信息。

柔性机构的物理参数包括密度、弹性模量、转动惯量等物理信息。柔性机构的外力参数包括驱动力、驱动力矩、阻抗力和阻抗力矩等力学参数。柔性机构的拓扑结构包括构件几何尺寸、相对位置和相对方位等。柔性机构的约束方式是指约束类型以及约束间隙数据、摩擦因数等。柔性机构的运动时域T是机构完成一次指定运动的时间,由启动、运行到定位各个时间段组成。

柔性机构系统动力学模型的建模方法主要有三种^[12-14,144]:牛顿-欧拉(Newton-Euler)方法、拉格朗日(Lagrange)方法和凯恩-休斯顿(Kane-Huston)方法。

1)牛顿-欧拉方法。又称为N-E方法,为向量力学法。该方法应用质心动量矩定理写出隔离体的动力学方程,在动力学方程中出现相临体间的内力项,其物理意义明确,并且表达了系统完整的受力关系,但是这种方法也存在着方程数量大、计算效率低等缺点,不过许多模型的规范化形式最终都是以该种模型出现,并且该方法也是目前动力学分析用于实时控制的主要手段。利用牛顿-欧拉方法对柔性梁建模时,假定柔性梁的变形和柔性梁的长度比较起来非常小;假设梁是具有均匀截面和稳定性质的欧拉-伯努利(Euler-Bernoulli)梁;梁的转动惯量和剪切变形忽略不计;空气阻力和梁的内阻尼忽略不计。

2)拉格朗日方法。为分析力学方法。该方法由拉格朗日方程或哈密尔顿原理出发,求出能量函数或哈密尔顿函数,以能量方式建模,可以避免方程中出现内力项,适用于比较简单的柔性体动力学方程,而对复杂结构,拉格朗日函数和哈密尔顿函数的微分运算将变得非常繁琐,但是变分原理又有其特点,由于它是将系统真实运动应满足的条件表示为某个函数或泛函的极值条件,并利用此条件确定系统的运动,因此这种方法可结合控制系统的优化进行综合分析,便于动力学分析向控制模型的转化。

3)凯恩-休斯顿方法。为达朗贝尔原理方法。该方法采用相对能量的形式,从约束质点系的达朗贝尔原理出发,将各体的主动力(矩)和惯性力(矩)乘以偏速度、偏角速度矢量,再对整个系统求和,可得到与系统自由度数目相同的方程组。其特点也是可消除方程中的内力项,避免繁琐的微分运算,使推导过程较为系统化,虚功原理与凯恩方法类似,在这种方法中颇具特色的当推凯恩-休斯顿方法,其采用低序体阵列描述系统的拓扑结构。

按照拉格朗日方法,建立柔性机构系统动力学方程:

式中 M(t)——柔性机构时变质量矩阵,M=diag(M₁,M₂,…,M_N);(www.xing528.com)

N——柔性机构系统内构件的数量;

K(t)——柔性机构时变刚度矩阵;

C(t)——柔性机构时变约束矩阵;

F(t)——柔性机构时变广义力矩阵;

λ——拉格朗日乘子列阵;

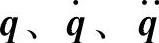——广义坐标;

T——柔性机构的运动时域,是指可靠性研究的时间范围。