柔性体模型及分析方法

柔性机构系统中的柔性构件一般为细长杆件、薄板件,在力学模型上通常作为柔性梁。对于包含有柔性体的机构系统,通过有限元方法将柔性体分割为有限个单元,将单元质量集中到节点上。

式中 Mⁱ——柔性机构系统内第i个柔性体的质量;

Mⁱ_j——第i个柔性体中第j个单元的质量;

n——第i个柔性体的单元数量。

柔性多体系统使用的坐标系与多刚体系统不同,这里采用浮动坐标系的形式建立柔性多体系统的坐标系,如图2-1所示。设柔性体任意节点Pⁱ在变形以后相对于柔性体质心Oⁱ的矢径为uⁱ,而未变形时Pⁱ处于矢径uⁱ₀的位置,节点Pⁱ的平移变形矢量为uⁱ_f。建立Ox₁x₂x₃坐标系,称为惯性坐标系,不随时间而变化;在柔性体的质心Oⁱ处建立Oⁱxⁱ₁xⁱ₂xⁱ₃坐标系,称为浮动坐标系,可以相对于惯性坐标系作有限的移动和转动。这样,柔性体上各点之间存在的相对变形,则用浮动坐标来表示^[2-4,144]。

图2-1中:Ox₁x₂x₃为惯性坐标系;Oⁱxⁱ₁xⁱ₂xⁱ₃为柔性体质心Oⁱ处的浮动坐标系;Pⁱ为柔性多体系统中第i个柔体上的任意节点;uⁱ表示节点Pⁱ在变形以后相对于柔性体质心Oⁱ的矢径,即相对于浮动坐标系的矢径;uⁱ₀表示节点Pi相对于浮动坐标系在零变形(变形前)时的相对位置矢量;uⁱ_f表示节点Pⁱ平移变形矢量。Rⁱ为柔性体质心Oⁱ相对于惯性坐标系原点O的矢径;rⁱ为节点Pⁱ相对于惯性坐标系原点O的矢径。

图2-1 系统的浮动坐标系

当柔性体作平面运动时,对于柔性机构系统中第i个柔性体上的任意节点Pⁱ,相对于浮动坐标系的矢径uⁱ和变形uⁱ_f可以表示为

uⁱ=uⁱ₀+uⁱ_f (2-2)

所以,相对于惯性坐标系的矢径rⁱ可以表示为

rⁱ=Ri+Aⁱuⁱ (2-3)

将式(2-2)代入式(2-3),得

rⁱ=Rⁱ+Aⁱ(uⁱ₀+uⁱ_f) (2-4)

其中,Aⁱ表示坐标变换矩阵:

式中,θ为浮动坐标系相对于惯性坐标系的转角。将uⁱ_f用模态函数矩阵和模态

坐标表示,有

uⁱ_f=Φⁱqⁱ_f (2-6)

式中 Φⁱ——相对于惯性坐标系的模态函数矩阵;

qⁱ_f——模态坐标。

如果相对于浮动坐标系的模态函数矩阵用Φⁱ_f表示,则

Φⁱ_f=(φⁱ_f1φⁱ_f2 … φⁱ_fs) (2-7)

那么柔性体相对于浮动坐标系的矢径可以表示为

uⁱ=uⁱ₀+Φⁱ_f+qⁱ_f (2-8)

将式(2-6)代入式(2-4),得到节点Pⁱ相对于惯性坐标系的矢径rⁱ为

rⁱ=Rⁱ+Aⁱuⁱ=Rⁱ+Aⁱ(uⁱ₀+Φⁱ_fqⁱ_f) (2-9)

为了缩减求解规模,一般情况下只需保留有限阶模态,即

Φⁱ=(φⁱ₁φⁱ₂ … φⁱ_s) (2-10)

qⁱ_f=(qⁱ₁qⁱ₂ … qⁱ_s) (2-11)

式中 s——保留模态的阶数。

通过上述方法,柔性体的位形就可以由浮动坐标系的笛卡儿坐标(x,y,z)和模态坐标q来描述了。

柔性体作平面运动时,柔性体上任意节点Pⁱ的速度可以由式(2-9)对时间求导得到,因为u₀和Φ_f为常值矩阵,所以

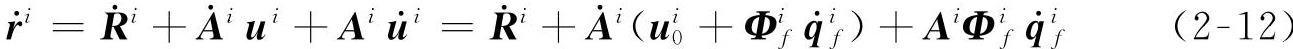
其中第二项可以用动坐标系旋转坐标对时间的导数来表示以便得到简洁的形式,即

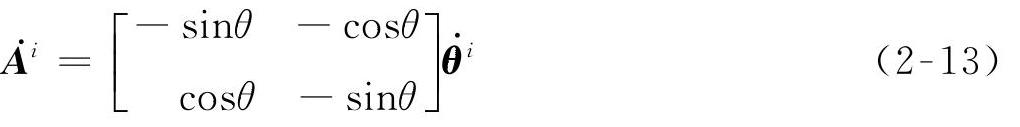
令

则

式中 ωⁱ——浮动坐标系相对于惯性坐标系的角速度。

柔性体任意节点的速度可以写为如下形式,在这里去掉上角标i,表示其适用于柔性机构系统中的任意柔性体。

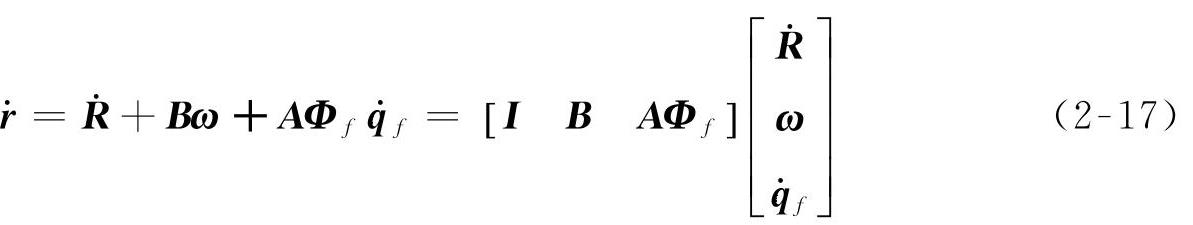
式中,AΦ_f可以转换为惯性坐标系的模态函数,Φ=AΦ_f;I为2×2单位矩阵。令

则式(2-17)可以简写为

式中,列阵具有速度量纲,由柔性体浮动坐标系的绝对速度、绝对角速度以及柔性体的模态速度组成。柔性体任意节点相对于浮动坐标系的速度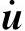由式(2-8)对时间求导得到,因为u₀和Φ_f为常值矩阵,所以

柔性体任意节点的加速度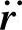由式(2-12)对时间求导得到,即

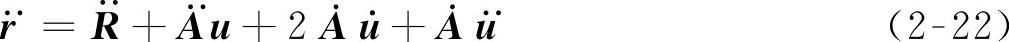
由于(www.xing528.com)

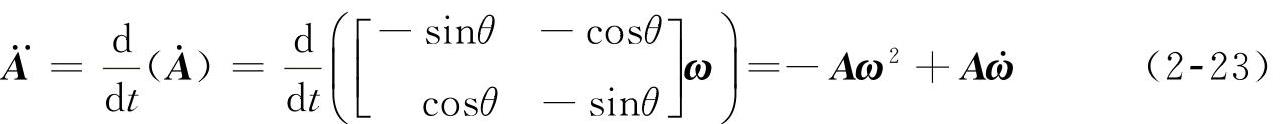
将式(2-8)、式(2-21)和式(2-23)代入式(2-22)可以得到相对于惯性坐标系的绝对加速度为

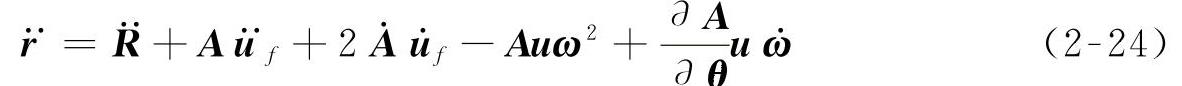
即

式中 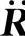——节点的牵连移动加速度;

——节点的相对变形加速度;

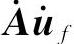——节点的科氏加速度;

-Auω²——节点的牵连转动法向加速度;

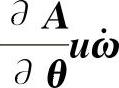——节点的牵连转动切向加速度。

柔性体任意节点相对于浮动坐标系的加速度由式(2-18)对时间求导得到,即

根据式(2-17)、式(2-18)和式(2-19)也可以将式(2-24)改写为模态函数和模态坐标的矩阵形式,即

柔性体的动能T为

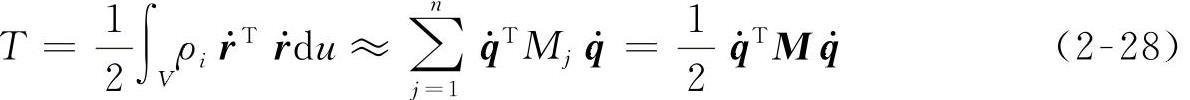
式中 ρ_i——柔性体的密度;

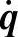——柔性体的广义坐标;

M——柔性体的广义质量矩阵。

这样,柔性体的广义质量矩阵就可以表示为

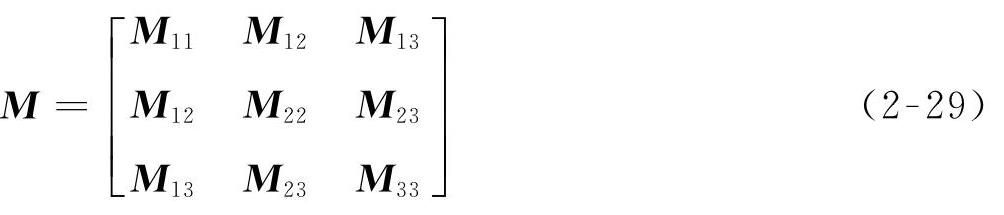
其中

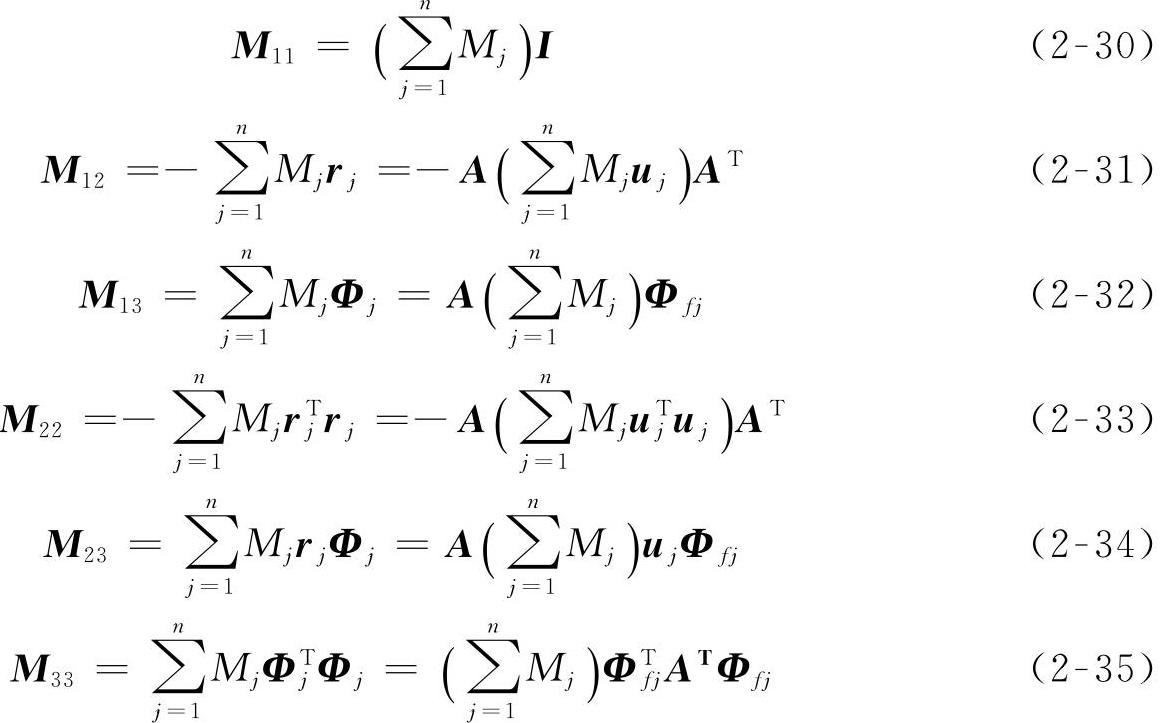
根据速度变分原理,平面柔性体的速度变分形式的动力学方程为

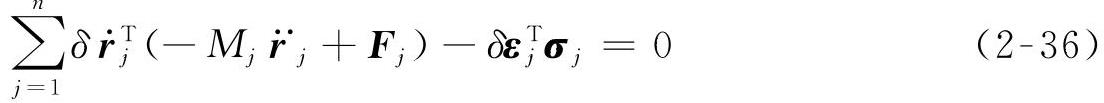
式中 F_j——作用于节点上的外力;

ε_j^T——单元应变;

σ_j——单元应力。

根据结构动力学的虚功原理,柔性体各个单元应力的总虚功为

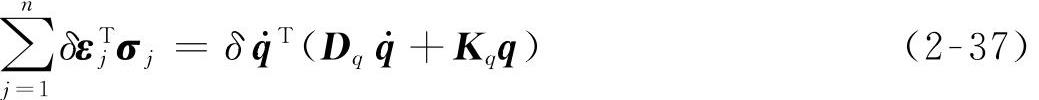
式中 D_q——模态阻尼矩阵,为常值矩阵;

K_q——模态刚度矩阵,为常值矩阵。

将式(2-20)、式(2-27)和式(2-37)代入式(2-36),整理得

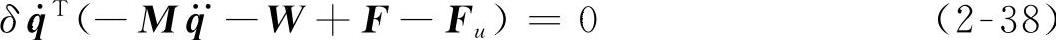
式中,M为柔性体的广义质量矩阵;W为柔性体的广义惯性力矩阵,且

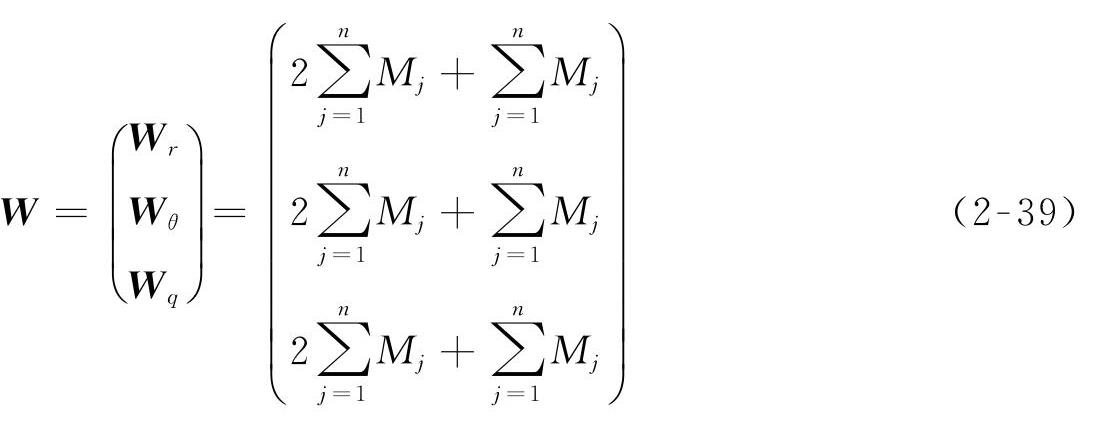
F为柔性体的广义外力矩阵,且

F_u为柔性体的广义变形力矩阵,且

对于空间柔性体描述,与平面柔性体描述方法类似,对柔性体进行有限元离散处理,用浮动坐标系的笛卡儿坐标和模态坐标表示空间柔性体的位形。有所不同的是在描述空间柔性体时,增加了反映空间柔性体方位的欧拉角,如图2-2所示。空间柔性体的位形由ξ来表示,即

ξ={x,y,z,φ,ϕ,θ,q}^T (2-42)

图2-2中,(x,y,z)为笛卡儿坐标,用于描述空间柔性体的位置;(φ,ϕ,θ)为欧拉角,用于描述空间柔性体的方位。

空间柔性体的动能T为

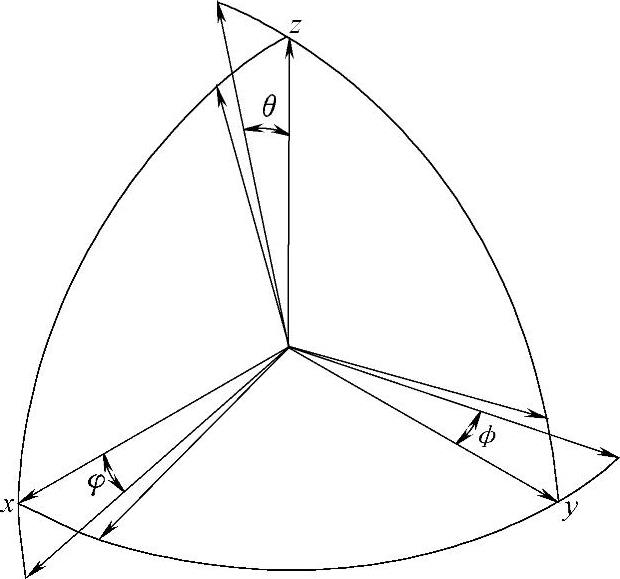
图2-2 惯性坐标系的笛卡儿坐标和欧拉角

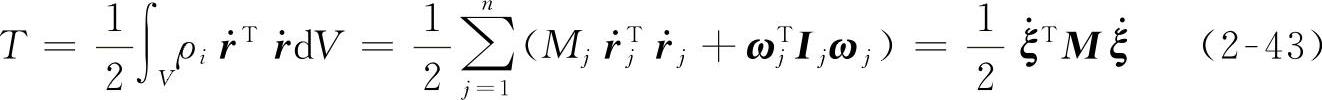
应用拉格朗日乘子法建立空间柔性体的动力学方程为

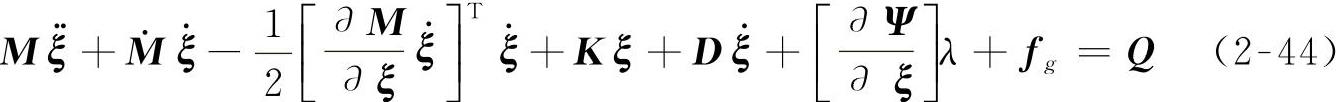
式中 D——阻尼矩阵;

f_g——重力;

Q——广义外力。

式(2-44)为微分代数方程(Differential Algebraic Equations,简称DAEs),一般情况下无法得到解析解,只能用数值方法求解。