粘土坡稳定性分析：地基与基础大揭秘

均匀土坡失去稳定时，沿着曲面滑动，如图5-28所示。通常滑动曲面接近圆弧面，在理论分析时可采用圆弧面计算。

1.条分法

图5-28　均质土坡滑动面

瑞典工程师弗伦纽斯（Fellenius，1992）假定最危险圆弧面通过坡脚，如图5-29（a）所示，并忽略作用在土条两侧的侧向力，提出了广泛用于粘性土坡稳定性分析的条分法。该法的基本原理是：将圆弧滑动体分成若干土条；计算各土条上的力系对弧心的滑动力矩和抗滑动力矩；抗滑动力矩与滑动力矩之比称为土坡的稳定安全系数；选择多个滑动圆心，通过试算求出多个相应的稳定安全系数，要求最小的稳定安全系数Kmin＝1.2～1.35。

具体分析步骤如下：

（1）按比例绘制土坡剖面图，如图5-29（a）所示，假设圆弧滑动面通过坡脚A 点，分析时垂直纸面取单位长度。

（2）任选一点O 为圆心，以OA 为半径作圆弧AC，AC 即为圆弧滑动面。

（3）将滑动土体ABC 竖直分成若干个等宽的（或不等宽的）土条，并对土条编号。编号时一般从圆心O 的铅垂线开始作为0 条，图中向右依次为1、2、3，…，向左依次为—1、—2、—3，…。为了计算方便，可取分条宽度为滑弧半径的1/10，即b＝0.1R，则此时sinβ1＝0.1，sinβ2＝0.2，…，sinβi＝0.1i，sinβ—i＝—0.1i 等，可减少大量三角函数计算。

（4）取第i 条作为隔离体进行分析，如图5-29（b）所示，计算该土条自重Gi＝γhibi（bi、hi、γ分别为计算土条的宽度、平均高度以及土的重度），分解Gi为滑动面ab（简化为直线段）上的法向分力Ni和切向分力Ti：

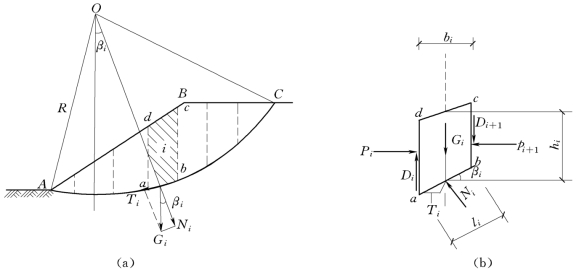
图5-29　土坡稳定分析的条分法

分析时不计土条两侧面ad，bc 上的法向力Pi、Pi＋1和剪切力Di、Di＋1的影响，其误差约为10%～15%。

（5）以圆心O 为转动中心，滑动面AC 上的滑动力矩等于各土条对弧心的滑动力矩之和，即

（6）圆弧滑动面对圆心O 的抗滑力矩，来自于法向分力Ni引起的摩擦阻力和粘聚力c 产生的抗滑力两部分。第i 土条的抗滑阻力T′i其可能发挥的最大值等于土条底面上土的抗剪强度与滑弧长度li的乘积，即

其抗滑力矩Mri为

则整个滑动面AC 上的抗滑力矩为

(www.xing528.com)

（7）计算稳定安全系数：

若取各土条宽度相等，上式可简化为

式中 φ——土的内摩擦角，（°）；

c——土的粘聚力，kPa；

βi——第i 土条ab 滑动面与水平面的夹角，（°）；

lAC——圆弧面AC 的弧长，m。

（8）由于滑动圆弧的圆心是任意选的，故上述计算结果不一定是最危险的。因此选择几个可能的滑动面（即不同的圆心位置），分别按上述过程计算相应的K 值，其中Kmin所对应的滑动面就是最危险滑动面。评价一个土坡的稳定性时，这个最小的安全系数值不应小于有关规范要求的数值。根据工程性质，规范要求最小的安全系数Kmin在1.2～1.35。试算工作量很大，可采用计算机求解。

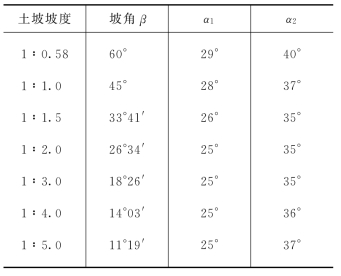
费伦纽斯通过大量计算，曾提出确定最危险滑动面圆心的经验方法。经验指出对于均质粘性土坡，最危险的滑动圆弧的圆心一般均在图5-30 中确定的DE 线上E 点的附近。E 点的位置由与坡角β有关的α1、α2角度确定（α1、α2值见表5-3），D 点位于坡脚A 点以下距离h，以右4.5h 处。当φ＝0 时，土坡最危险滑动面的圆心在E 点，当φ＞0 时，圆心在DE 线E 点向上附近，可用试算法确定，即在DE 延长线上分别取圆心O1、O2、…，绘出相应的通过坡脚的滑弧（图中未绘出），计算相应的稳定安全系数K，并在DE 线的垂直方向绘出K 值曲线，曲线最低点即为所求的最小安全系数Kmin，相应的圆心Omin为最危险滑动面圆心。对于非均质粘性土土坡，或坡面形状及荷载情况都比较复杂，这样确定的Kmin还不甚可靠，尚需自Omin点作DE 线的垂线，在其上的Omin附近再取圆心O′1、O′2、O′3、…，按照同样的方法进行计算比较，才能找出最危险滑动面的圆心和土坡的最小安全系数。

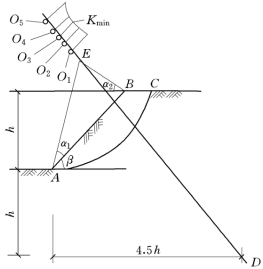
图5-30　最危险滑弧圆心的确定

　表5-3　α1和α2的数值

2.图表法

对于简单粘性土土坡的稳定性分析，为了减少繁重的试算工作量，曾有不少人寻求简化的图表法。根据大量的计算资料整理，以坡角β为横坐标，稳定因数为纵坐标绘制的一组曲线，如图5-31所示，就是最简单的一种，它是极限状态时均质土坡内摩擦角φ，坡角β与稳定因数N 之间的关系曲线，可用来解决如下两类问题：

（1）已知坡角β、土的内摩擦角φ、土的粘聚力c 和土的重度γ，求最大边坡高度h。这时，可由β、φ，查图5-31 得N，则

（2）已知c、φ、γ、h，求稳定坡角β，这时可由和φ查图5-31得β。

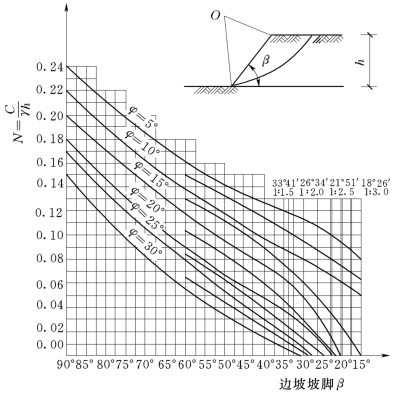
图5-31　粘性土简单土坡计算图