地基与基础中的主动土压力

如图5-7所示，当楔体ABM 向下滑动处于极限平衡状态时，作用在楔体上的力有：

1.楔体重力G

由土楔体ABM 自重引起，只要破坏面AM 的位置一确定，G 的大小就是已知的，方向向下，根据几何关系可得

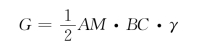
在三角形ABM 中，由正弦定理得

又因

故

2.AM 面反力R

为滑动破坏面的法向分力与破坏面上土体间的摩擦力的合力，其大小是未知的，但其方向则是已知的。反力R 与破坏面AM 的法向方向N1之间的夹角为土的内摩擦角φ，当楔体下滑时，位于N1的下侧。

3.墙背反力E

它与作用在墙背上的土压力大小相等，方向相反。反力E 与墙背AB 的法向方向N2呈δ角，δ角为墙背与填土之间的摩擦角，称为外摩擦角。当楔体下滑时，墙对土楔的阻力是向上的，故E 位于N2的下侧。

土楔体ABM 在上述三力作用下处于静力平衡状态，因此三力必构成一闭合的力矢三角形 [图5-7（b）]，由正弦定理得

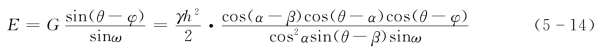
其中

(www.xing528.com)

上式中γ、h、α、β、φ及δ都是已知的，而滑动面AM 与水平面的夹角θ则是任意假定的，因此，假定不同的滑动面可以得出一系列相应的土压力E 值，即E 是θ的函数。只有相应于E 最大值Emax时的θ角倾斜面才是真正的滑动破坏面，相应的Emax才是所求墙背上的主动土压力。可用微分学中求极值的方法求得E 的极大值，即令从而解得使E 为极大值时填土的破坏角θcr，这才是真正滑动破坏面的倾角。将θcr代入式（5-14），经整理可得库仑主动土压力的一般表达式：

其中

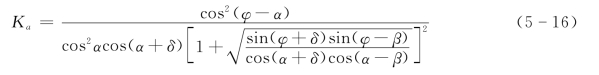
式中 α——墙背与竖直线的夹角，（°），俯斜时取正号，仰斜时取负号；

β——墙后填土面的倾角，（°）；

δ——土与墙背材料间的外摩擦角，（°）；

Ka——库仑主动土压力系数，可由上面的公式计算，也可查表。

当墙背直立（α＝0）、光滑（δ＝0）、填土面水平（β＝0）时，式（5-16）变为

可见满足朗肯理论假设时，库仑理论与朗肯理论的主动土压力计算公式相同。

墙顶以下任意深度z 以上的主动土压力由式（5-15）可得，为

将上式对z 求导数，得到主动土压力强度沿墙高的分布计算公式：

可见库仑主动土压力强度沿墙高呈三角形分布[图5-7（c）]，Ea的作用方向与墙背的法线夹角为δ，作用点距墙底h/3 处。必须注意图中所示的土压力分布图只表示其大小，而不代表其作用方向。