1.基本概念
如果挡墙在外力作用下向右挤压土体,如图5-3(c)所示,竖向应力σz仍不变,而水平应力σx随着挡墙位移增加而逐渐增大,当σx超过σz时,σx变为大主应力,σz则变为小主应力,直到挡墙位移达到Δp时,土体达到被动极限平衡状态,σx达最大值,莫尔应力圆与抗剪强度包线相切,如图5-3(d)中圆Ⅲ所示。土体形成一系列剪切破坏面,此种状态称为朗肯被动状态。此时墙背上水平应力σx为最大主应力,即朗肯被动土压力强度σp。因土体处于朗肯被动状态时,大主应力作用面是竖直面,故剪切破坏面与水平面的夹角为![]()
2.计算公式
如前所述,当挡土墙在外力作用下向右挤压土体达到被动朗肯状态时,墙背上任一深度z 处的被动土压力强度为极限平衡状态时的大主应力,即σp=σ1,与其相应的小主应力σ3=γz,于是由式(5-3a)和式(5-4a)可得朗肯被动土压力强度为

上二式中 Kp——被动土压力系数,![]()
其余符号同前。
由式(5-10)和式(5-11)知,无粘性土的被动土压力强度呈三角形分布[图5-5(b)],粘性土的被动土压力强度则呈梯形分布 [图5-5(c)]。如取单位墙长计算,则被动土压力Ep为
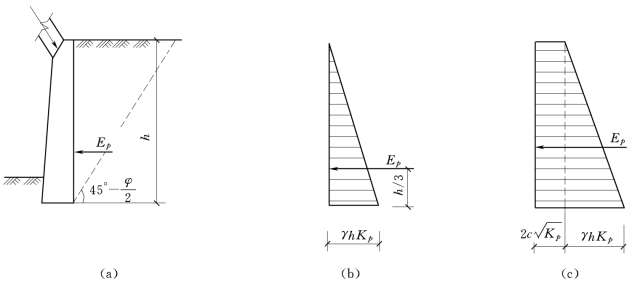
图5-5 朗肯被动土压力分布
(a)被动土压力图式;(b)无粘性土;(c)粘性土
粘性土

无粘性土
![]() (https://www.xing528.com)
(https://www.xing528.com)
Ep通过三角形或梯形压力分布图的形心。
朗肯土压力理论应用弹性半空间体的应力状态,根据土的极限平衡理论推导和计算土压力。其概念明确,计算公式简便,但由于假定墙背竖直、光滑、填土面水平,使计算条件和适用范围受到限制,计算结果与实际有出入,所得主动土压力值偏大,被动土压力值偏小,其结果偏于安全。
【例5-1】 某挡土墙高6m,墙背直立光滑,填土面水平。填土的物理力学性质指标为c=10kPa,φ=20°,γ=18kN/m3,试求主动土压力及作用点,并绘出土压力强度分布图。
解 由已知该墙满足朗肯条件,故可按朗肯土压力公式计算沿墙高的土压力强度:
![]()
墙顶处


图5-6 主动土压力分布图
因在墙顶处出现拉力,故须计算临界深度z0,由式(5-5)得

土压力分布图如图5-6所示,其主动土压力Ea为
![]()
Ea作用点距墙底的距离为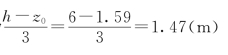
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




