地基与基础：渗透固结与时间的关系

渗透固结是指饱和粘性土在压力作用下孔隙水向外排出的时间过程。

对于地基的变形，上一节我们讲的是最终变形量，产生最终变形量的时间长短即固结速度与土体的渗透性、周边排水条件以及土的压缩性等有关，主要是土体的渗透性，对于砂土和碎石土等压缩性小、渗透性强的土体，固结稳定所需时间很短，而对饱和的粘性土而言，固结稳定所需时间很长，对于这种情况，往往还需了解其一定时间内的变形量。

1.两类问题

对于渗透固结与时间的关系，一般需要解决两类问题，即求某一时间t 的变形量st或求某一变形量st所需的时间t。

2.固结度概念

固结度是指土层在固结过程中任一时刻的压缩量st与最终压缩量s 之比，即

因最终压缩量s 可由上节的分层总和法或规范法求得，所以只要知道Ut和时间t 的关系，便可解决上述两类问题。

3.Ut和t 的关系

根据太沙基一维渗透固结理论，对于一定假设条件下的固结情况，可得固结度Ut与时间t 的关系。

基本假设：①土是均质的、完全饱和的；②土粒和水是不可压缩的；③土层的压缩和土中水的渗流只沿竖向发生，是单向（一维）的；④土中水的渗流服从达西定律，且土的渗透系数K 和压缩系数a 在渗流过程中保持不变；⑤外荷载是一次瞬时施加的。

Ut和t 的关系可通过中间变量时间因数Tv联系起来，即Ut—Tv—t。

（1）Tv与t 的关系。Tv与t 的关系可通过以下公式换算：

式中 Cv——土的固结系数，cm2/年；k 为渗透系数，e1为土的初始孔隙比，a 为压缩系数；

H′——压缩土层中孔隙水的最大渗径，单面排水时为土层厚度，即H′＝H，双面排水时为土层厚度之半，即H′＝H/2。

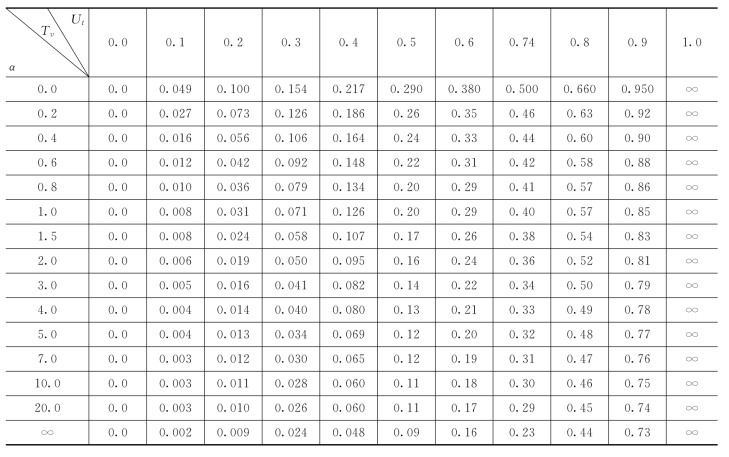
（2）Ut与Tv的关系。Ut与Tv的关系可由表3-12 查得，表中α值的确定方法：①单面排水时，即透水侧的附加应力值与不透水侧的附加应力比值；②双面排水时α＝1。

表3-12　单面排水不同α下的Ut—Tv关系表

4.解决两类问题的步骤

（1）已知土层的最终变形量s，求某一固结历时t 的变形量st。

1）由资料k、a、e1求固结系数Cv，

2）求时间因数Tv：

3）确定α：（双面排水时α＝1）；(www.xing528.com)

4）由α和Tv查表3-12 得Ut；

5）求st：st＝sUt。

（2）已知土层的最终变形量s，求土层达到某一变形量st时所需的时间t。

1）求Ut：

2）确定（双面排水时α＝1）；

3）由Ut和α查表3-12 得Tv；

4）求Cv：

5）求

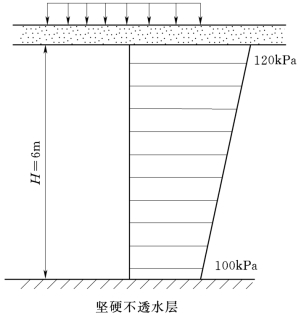
图3-18　单面排水基底附加应力分布

【例3-7】 某基础基底中心点下的固结应力分布如图3-18所示。地基系饱和粘土层，厚度H＝6m，其底面为坚硬不透水层，压缩系数a ＝0.4MPa—1，初始孔隙比e1＝0.8，渗透系数k ＝0.014m/年。试求：①加荷1年后地基的变形量；②地基的固结度达80%时需多少时间？

解（1）计算地基最终变形量。该土层固结应力平均值为

粘土层的最终变形量为

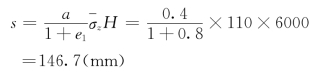
（2）加荷1年后的地基变形量。土的固结系数为

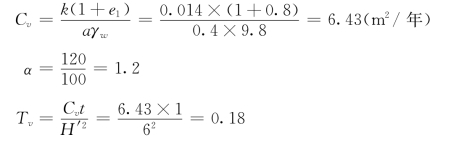
查表3-12，加荷1年后地基固结度Ut＝0.48，

因此

（3）Ut＝80%时所需时间。由α＝1.2，Ut＝0.8，查表3-12 得Tv＝0.56，则