自动化集装箱码头设计与仿真：主要事件、活动与进程

自动化集装箱码头的水平运输环节仅仅包含装船和卸船两个进程。装船进程起于场桥终于岸桥，而卸船进程则正好相反。当采用不同种类的车辆时，码头的装船进程和卸船进程略有区别。为了描述进程中的异步关系，本部分以Petri网表达三种车辆的装船和卸船进程。

1.Petri网简介

Petri网是一种描述离散并行系统的有效手段。基本Petri网由库所（place）、变迁（transaction）、有向弧（arcs）组成，分别以圆、矩形和有向箭头表示；网内往往存在若干令牌（token），一般以圆点表示。库所是令牌的容器，可能具有一定的容量，对应自身令牌的最大数量。有向弧是令牌的管道，定义了令牌的流向，以及一次通过有向弧的令牌数量。有向弧可能从库所指向变迁，也可能反过来由变迁指向库所；前一种情况下，库所是变迁的输入，后一种情况下，库所则是变迁的输出。变迁是令牌的阀门，可能具有保护函数（guard function），对令牌的流动进行限制。假设Petri网内的某个变迁，以及若干与之相连的输入库所和输出库所，当所有输入库所都存在足够数量的令牌时，变迁被击发（firing），所有输入库所内的令牌数量按照有向弧规定的数量减少，所有输出库所内的令牌数量则按照有向弧规定的数量增加。令牌总是按照库所、变迁和有向弧的定义在网内流动，对应整个Petri网的各种可能状态和状态变化。

Petri网是表达离散事件仿真模型的有效工具。离散事件仿真由实体、属性、状态、事件、活动、进程六个要素组成，这些要素均能够以Petri网的概念进行表达：令牌对应于实体，库所对应于属性，令牌所在的库所对应于状态；变迁的击发对应于事件的触发，令牌在库所中的停留对应于活动的进行，库所与变迁相连又形成仿真的进程。Petri网概念与仿真六要素的对应关系见表8-1。

表8-1　仿真六要素的Petri网概念表达

图8-14给出了一个简单的Petri网示例。该Petri网由5个库所、3个变迁和8个有向弧组成，一共包含4个令牌，且图中各有向弧每次通过的令牌数量均为1。图中的库所P1 、 P2和P3，以及变迁T1 和 T2属于同一个进程（进程1）；同时库所P4和P5以及变迁T3属于另一个进程（进程2）。图中变迁T1的击发条件已经满足，因此令牌A将从库所P1中消失，同时一个新的令牌将被添加到库所P2。图中变迁T2的击发条件也已满足，因此令牌B和C将分别从库所P2和P6中消失，同时一个新的令牌将被添加到库所P3。

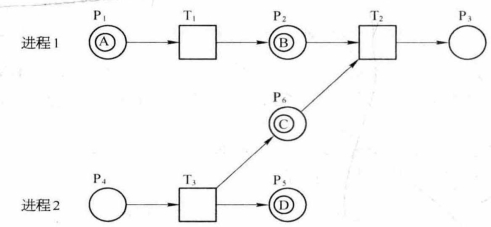
图8-14　简单Petri网示例

Petri网能够清晰地描述离散系统内的并发和异步关系。Petri网内的所有令牌都是独立个体，因此同一进程的令牌之间天然具有并发关系，例如图8-14中的令牌A和令牌C。异步关系一般以多个进程之间的连接库所表示，作为进程之间的一种记录。以图8-14中的库所P6为例，该库所游离于两个进程之外，因此令牌B和令牌D并不强制要求同步通过某些变迁。然而，在库所P6中没有令牌，或者令牌数量到达最大值的情况下，进程1或进程2中的某些令牌可能需要暂时等待。

2.车辆的装船和卸船进程

自动化集装箱码头的装船和卸船进程因水平运输车辆类型的不同而略有差异。对于没有自主装卸能力的车辆（如AGV），装船和卸船进程中要求起重机和车辆同步进行交接，因此起重机和车辆间容易发生等待；对于具有自主装卸能力的车辆（如ASC），装船和卸船进程中车辆和起重机的交接可以异步进行，因此起重机和车辆之间相互等待的情况能够极大缓解。鉴于同种车辆的装船进程与卸船进程基本一致，因此各车辆的卸船进程不再赘述。

采用AGV的水平运输系统的装船进程如图8-15所示，各库所和变迁的含义见表8-2。该进程中场桥和岸桥的进程与车辆进程重叠，变迁T3要求车辆和场桥全都交接点才能击发，否则令牌无法进入库所P5，集装箱交接无法进行。变迁T7亦要求车辆和岸桥全都到达交接点才能击发。车辆与场桥、车辆与岸桥任意一方的迟到，都将引起另一方在交接点等待。

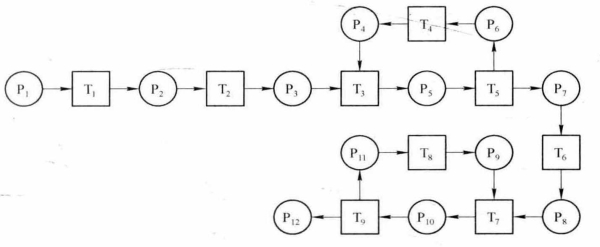
图8-15　采用AG V的水平运输系统的装船进程

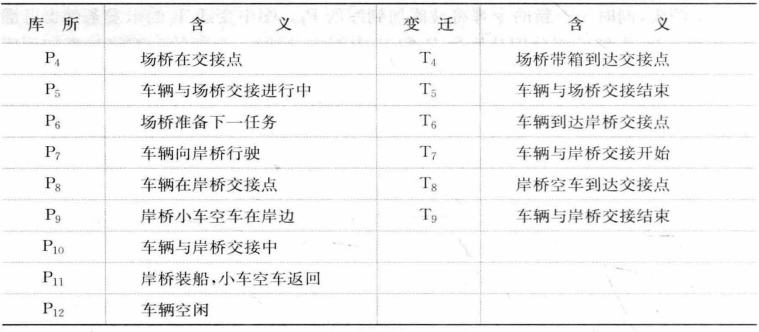
表8-2　采用AGV的水平运输系统Petri网元素列表

（续表）

采用ALV的水平运输系统的装船进程如图8-16所示，各库所和变迁的含义见表8-3。注意图中库所P6的容量为Y（场桥支架的容量），其余库所容量均为1。该进程中场桥的进程从车辆进程中脱离，变迁T5的击发并不要求场桥处在交接点。然而，岸桥的进程并未从车辆进程中脱离，变迁T8仍要求车辆和岸桥全都到达交接点才能击发，因此车辆的迟到将引起岸桥等待。(www.xing528.com)

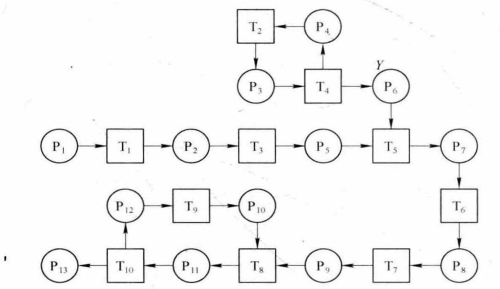
图8-16　采用ALV的水平运输系统的装船进程

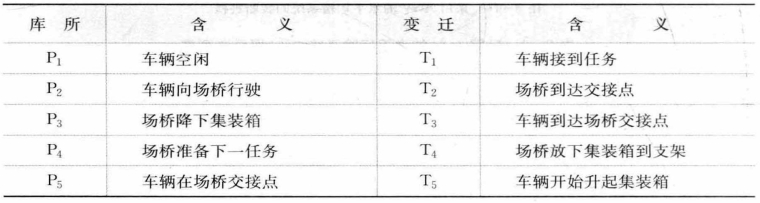
表8-3　采用ALV的水平运输系统Petri网元素列表

（续表）

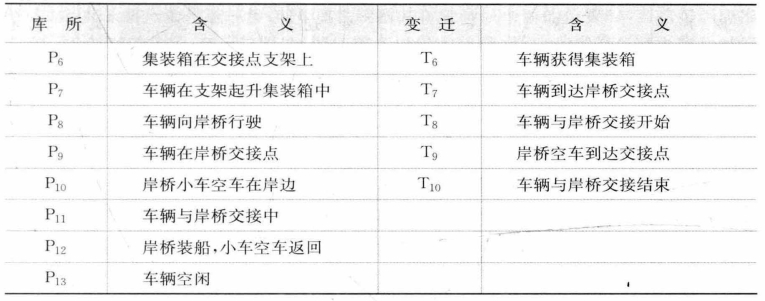
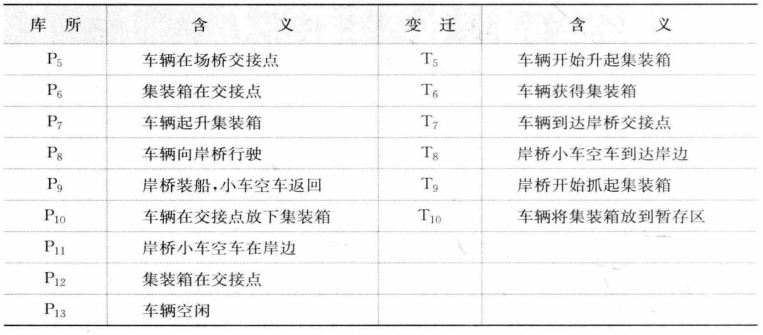
采用ASC的水平运输系统的装船进程如图8-17所示，各库所和变迁的含义见表8-4。注意图中库所P6的容量为Y（场桥暂存区容量），库所P12的容量为Q（岸桥暂存区容量），其余库所容量均为1。该进程中，场桥和岸桥的进程均从车辆进程中脱离，变迁T5的击发并不要求场桥处在交接点，T10的击发也不要求岸桥小车空车处在岸边。因此，该进程内车辆的一两次迟到，一般不会引起场桥或者岸桥的等待。

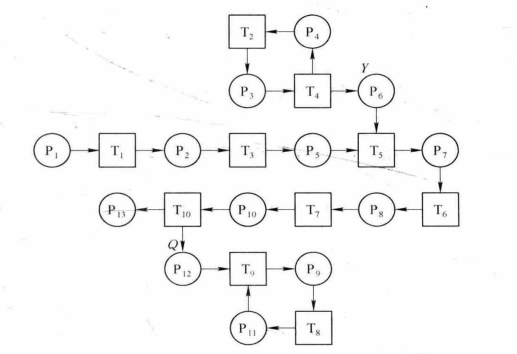
图8-17　采用ASC的水平运输系统的装船进程

表8-4　采用ASC的水平运输系统Petri网元素列表

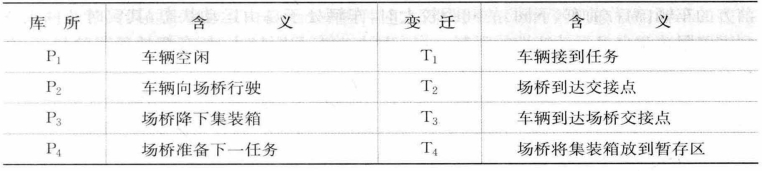
（续表）

3.车辆行驶的微观交通仿真

车辆在岸桥和场桥之间的行驶时间始终受到实时交通的影响。即使由调度给定了车辆的起点和终点，并由路径规划给定了两点间的行驶路径，车辆也不可能沿着路径全速前进，始终会因安全行驶的目的而控制实时速度。因此车辆在起点到终点间的行驶时间并非由车辆自身决定，且难以用数学模型的方式进行描述。因此，对于车辆行驶过程的仿真，仍需要合适的方法。

微观交通仿真是交通仿真领域的一种常用方法，能够体现车辆行驶过程中的速度变化，能用于模拟车辆在码头物流系统交通网络中的行驶过程。微观交通仿真是关注交通系统细节的仿真方法，能够对系统中所有个体的特性、行为和具体过程进行描述。微观交通仿真方法具有明确的车辆和路网定义，以单个车辆为基本研究单元，对系统中所有车辆个体都进行标示和定位。微观交通仿真本质上是一类特殊的离散事件仿真方法，系统模型中存在确定长度的基本时间单位（扫描时段），仿真钟按照该时间单位进行推进；系统中的事件均发生在扫描时段末尾，事件中车辆的速度、加速度和其他属性的实时状态将被更新。微观交通仿真一般用于研究交通流与局部道路设施的相互影响，也可用于研究交通控制策略。

微观交通仿真模型通常由两部分组成。第一部分是对交通设施和路网几何形状的精确描述，可能包括信号灯、检测器和信息指示牌等交通设施。第二部分是对每辆车动态交通行为的精确模拟。根据微观交通理论，车辆在交通系统中的行驶过程可以用自由运动状态和跟驰状态进行描述。当车辆轨迹前方不存在其他车辆，或者车辆与轨迹前方的车辆（简称前车，下同）的间距较大时，车辆处于自由运动状态，其实时速度仅受到道路限速和自身运动特性的限制。当车辆与前车间距较小时，车辆处于跟驰状态，其实时速度还受到前车运动状态的限制。

安全距离模型是一类常用的跟驰模型。这类模型旨在确定车辆与前车之间的最小间距，以保证车辆与前车之间总是不会发生碰撞。最著名的安全距离模型当属美国联邦公路局（Federal High Way Administration， FHWA）开发的NETSIM模型。该跟驰模型被广泛用于多种微观交通仿真模型，如VISSIM、 STEPS等。该模型的逻辑可以描述为：当仿真钟向前推进一步，前车属性刷新并行驶到一个新的位置时，当前车辆应推进到一个特定的位置；在该位置处，即使前车以最大减速度停车，当前车辆也能及时停车从而避免碰撞。按此逻辑可以保证，任何情况下车辆都不会与前车追尾。