自动化集装箱码头设计与仿真技术

本文介绍的自动化集装箱码头中常用的概率分布主要是在实践中对于不同的随机事件使用较多的概率分布情况。对于不常发生的随机事件，或者对于特定的系统，某些随机事件发生具有特殊性则需要详细的统计数据，通过分布类型假设检验来确定适用的分布类型，并使用最大似然法等估计方法估计分布的参数。

1.船舶达到间隔时间概率分布

指数分布由于其指数项系数为负值因而又称为负指数分布（negexp distribution）。泊松事件流的等待时间（相继两次出现随机事件之间的间隔）服从指数分布。指数分布常用于描述随机事件发生的间隔时间，例如排队系统中“顾客”到达系统的间隔时间。因此，指数分布适用于描述自动化集装箱码头船舶到达间隔时间。

指数分布（负指数分布）在x＞0值域上概率密度函数为

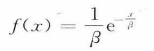
其中，β为均值。

【例5-5】经统计，某码头集装箱船舶到达情况见表5-4。已知该码头年工作时间为345 d，年吞吐量150万TEU，求该码头船舶到达间隔时间概率密度函数。

表5-4　船型比例及装卸量

由表5-4可计算平均每条船舶装卸量数学期望：1727.1 TEU。依据年吞吐量可计算一年平均到达船舶艘次：881.19艘。依据码头年作业天数345 d可计算船舶平均到达间隔时间：9.39 h。所以该码头船舶到达时间间隔规律服从均值为9.39 h的负指数分布。

2.船舶装卸量概率分布

每条集装箱船舶在集装箱码头的装卸量根据不同的船型随机变化。一般载箱量大的船型，在每个港口的装卸量也比较大。同时在一个航线上不同地位的港口船舶的装卸量也不同，对于国际中转港集装箱装卸量通常较大，对于支线补给港集装箱船舶装卸量通常较小。因此，不同码头、不同船型船舶装卸量概率分布不同，可以根据每个港口不同船型装卸量的统计数据进行分析。通常同一个集装箱码头同一种载箱量船型其装卸量按照标准正态分布（normal distribution）随机变化。

3.外集卡到达时间概率分布

来往集装箱码头的外集卡主要有两类作业任务：提箱和集港。对于集港和提箱作业的外集卡，通常集装箱码头对每一航次集港和提箱作业都分别规定开始时间和截止时间，货主在组织外集卡集港时都尽量赶在截止日期前的一段时间送达，而提箱作业则尽量在开始后不久到达。从集装箱码头外集卡到达的时间统计可发现集港作业和提箱作业外集卡到达时间呈三角分布规律。

【例5-6】 统计某集装箱码头十个航次集港时外集卡到达在各个时间段内分布情况见表5-5。假设该集装箱码头集港开始时间从第0h开始至第120 h结束。求该集装箱码头外集卡集港到达时间分布规律。并设计计算仿真中该码头集港时外集卡到达时间随机函数。

表5-5　某集装箱码头统计外集卡集港到达分布

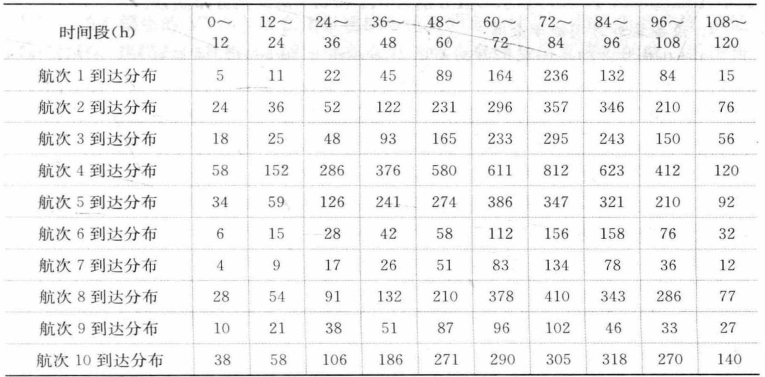
根据表5-5，计算各时间段累计时间占比及各时间段平均到达集卡数量，见表5-6。将表5-6绘制成柱状图，如图5-5所示，其中横坐标表示各时间段在整个集港阶段中所处百分比，纵坐标表示统计的十个航次中，该时间段内平均到达外集卡数量。由图5-5可见，该集装箱码头集港作业时外集卡到达时间服从三角分布，该三角分布起始时间为0，终止时间为120 h，峰值时间为72～84 h，该时间段处于整个集港时间中的70%左右。因此，可设计该集装箱码头外集卡集港时间计算函数如下：

表5-6　各时间段累计时间占比及平均到达集卡数

(www.xing528.com)

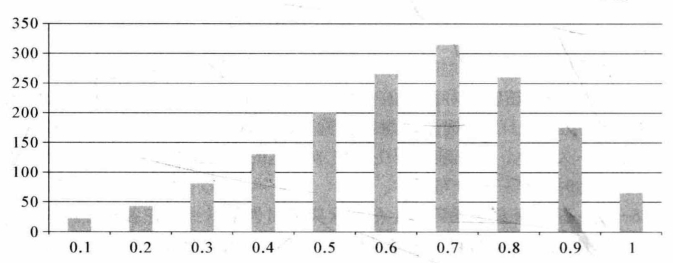
图5-5　各时间段内外集卡平均到达数

任意外集卡集港到达时间=开始时间+triangle（0， 1， 0.7）×120 h

其中，triangle（0， 1， 0.7）表示参数分别为0、1和0.7的三角分布函数。

4.设备装卸时间概率分布

自动化集装箱码头中各类设备在设定的参数下，装卸时间通常具有一个相对固定的均值。在自动化集装箱码头仿真中，如果仿真精度不要求细致到刻画设备装卸时内部机构的具体运动动作轨迹，例如相对简化的宏观仿真，则可将设备装卸时间用相对简单的概率分布模拟，通常可以针对不同种类及型号，使用标准正态分布来模拟。

5.设备故障间隔及修复时间概率分布

在自动化集装箱码头系统仿真中，通常设备故障间隔时间可以使用威布尔分布来模拟。威布尔分布在x ＞ 0值域内概率密度函数为

上式中涉及形状参数α ＞ 0；比例参数β＞ 0；这两个参数可以使用最大似然法进行估计：

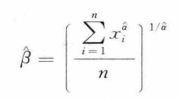
对于设备故障后的维修时间则可以使用伽马分布或者简单使用标准正态分布来模拟。其中，伽马分布在x＞0值域内概率密度函数如下：

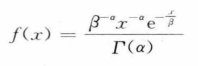
其中，Γ（α）为伽马函数（见5.4.4的内容）。

涉及形状参数a＞ 0；比例参数β＞0；可以使用以下最大似然法进行估计：

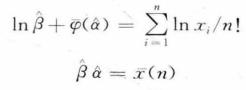
其中，φ（â）=Γ′（â）/Γ（â），Γ′（â）为Γ（â）的导数。