自动化码头设计与仿真：随机变量生成原理

随机数的产生介绍的是如何生成［0，1］区间内的均匀分布的随机数，随机变量的生成原理将进一步介绍如何使用［0，1］区间内的均匀分布随机数生成其他分布类型的随机变量。

1.逆变法

逆变法以概率积分变换定理为基础，假设要产生的随机变量X是连续的，其分布函数为F（x），则F（x）也是连续的，且在0＜ F（x） ＜ 1时单调递增；令F′（u）是F（x）的反函数，因为F（x）的值域为［0，1］，所以u∈［0，1］；若U是［0， 1］区间均匀分布的随机变量，则随机变量

Y=F-1 （U）

同X具有相同的分布函数，这是因为

P（Y ≤ y） =P（F-1 （U） ≤ y） = P（U ≤ f（y）） = F（y） = P（x ≤ y）

利用这一结论，首先产生［0， 1］区间均匀分布U，然后令y=F-1 （U），则Y就是一个服从给定分布F（x）的随机数。

【例5-3】 求服从指数分布的随机数x。

指数分布密度函数f（x）=λe-λx（x≥0），分布函数为

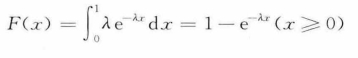
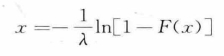
其反函数为

设u为［0， 1］均匀分布随机变量，则

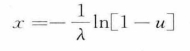
即为所求随机变量。因为u为［0， 1］均匀分布随机变量，1-u也为［0， 1］均匀分布随机变量，所以上式简化为

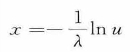
2.组合法

当一个分布函数可以表示成若干个其他分布函数之和，而这些分布函数较原来的分布函数更易求得其随机变量时，可以采用组合法。

首先介绍凸组合的概念，它的定义如下：设x1，x2，…，xk是Rn中点集X的k个点，若存在λ1， λ2 ， …， λk满足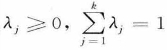，使

x′ = λ1 x1 +λ2x2 + … + λkxk(www.xing528.com)

也属于X，则称x′为x1， x2， … ， xk对于λ1，λ2， … ，λk的凸组合。

组合法的主要思想是：当要生成的随机变量服从的分布函数可以使用其他分布函数F1， F2， … ，Fk的凸组合表示时，若每一个Fj的随机变量求解远比F的求解简单，则可以先产生服从Fj的随机变量，然后再利用这些随机变量产生服从F的随机变量。具体来说，假设对所有x， F（x）可以写成

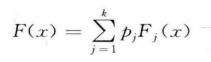
这里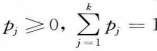；每个Fj都是一个分布函数。同样若x有密度函数f（x）可以写成

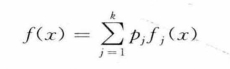
这里fj是其他密度函数。那么这k个分布的组合，具有密度函数f（x）的随机变量可以用下列算法生成：

①定义累计函数：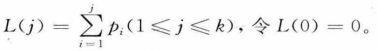

②随机变量发生器生成两个独立的［0， 1］均匀分布的随机变量u1和u2。

③若L（j-1） ＜u1 ＜L（j），则F（x）的随机变量从概率密度函数fj（ x）中产生，即根据u2获得服从fj（x）的随机变量xj，并取x=xj。以后的随机变量依次按照上述方法产生并输出。

组合法的集合解释是：对于X上的一个具有密度f的连续随机变量，可以将f下的面积分为p1， p2， …区域，对应于将f分解为凸组合表示，然后可以首先选择一个域再从所选域对应的分布中产生随机变量，最后将这些随机变量组合为所要求的随机变量。

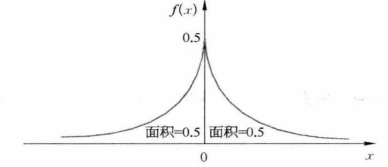
图5-4　双指数分布密度函数

【例5-4】 设存在一个分布，其密度函数f（x） = 0.5e- |x|（双指数分布如图5-4所示），求服从该分布的随机变量x 。

显然直接用逆变法产生随机变量难度比较大，此时采用组合法则相对简单。f（x）可以看作是一个正指数分布和负指数分布组合：

f（ x） = 0.5ex I（- ∞，∞ + ） （x） +0.5e-xI（ -∞， +∞） （x）

这里IA（x）是集合A的指示函数，定义为

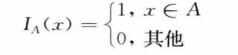
因此，f（x）可以看作f1 （x） = 0.5ex I（-∞，+∞）（x）和f2（x） = 0.5e-xI（-∞，+∞）（x）的凸组合，f1 （x）和f2（x）都是密度函数，且p1 = p2 =0.5，因此可以通过f1 （x）和f2（x）组合来产生服从密度函数f（x）的随机变量X。首先产生两个独立的［0， 1］均匀分布U1和U2，如果U1 ≤0.5，择取X为密度为f1（x）的随机变量，即令X=-ln U2，如果U1 ＞0.5，则取X为密度为f2（x）的随机变量，即令X=lnU2。