直流电路，欧姆定律和混联电路简介

（1）电路及基本物理量

电路就是电流的通过路径。最基本的电路由电源、负载、连接导线和开关等组成，如图3-27所示。电路分为外电路和内电路。从电源一端经负载回到另一端的电路称为外电路。电源内部的通路称为内电路。

1）电流。导体中的自由电子在电场力的作用下，做有规则的定向运动，就形成了电流。习惯上规定正电荷的移动的方向为电流的方向。每秒内通过导体截面的电量多少，称为电流。用I表示，单位为安培，简称安（A），即

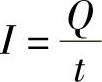
式中 I——电流，单位为A；

Q——电量，单位为C；

t——时间，单位为s。

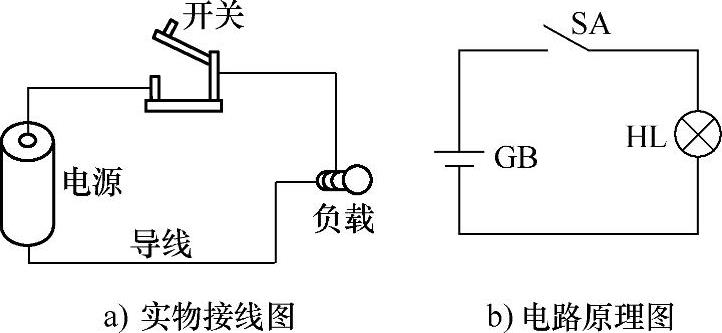
图3-27 电路图

2）电流密度。通过导线单位截面积的电流。

3）电压、电位。电位在数值上等于单位正电荷沿任意路径从该点移至无限远处的过程中电场力所做的功。其单位为伏特，简称伏（V）。

电压就是电场中两点之间的电位差。其表达式为

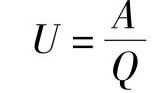
式中 A——电场力所做的功，单位为J；

Q——电荷量，单位为C；

U——两点之间的电位差，即电压，单位为V。

4）电动势。在电场中将单位正电荷由低电位移向高电位时外力所做的功称为电动势，其表达式为

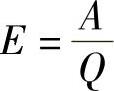
式中 A——外力所做的功，单位为J；

Q——电荷量，单位为C；

E——电动势，单位为V。

电动势的方向规定为由负极指向正极，由低电位指向高电位，且仅存于电源内部，如图3-28所示。

5）电阻。电流在导体中流动时所受到的阻力，称为电阻。用R或r表示。单位为欧姆（Ω）。导体电阻的大小与导体的长度L成正比，与导体的截面积成反比，并与其材料的电阻率成正比，即

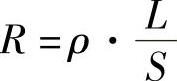
式中 ρ——导体的电阻率，单位为Ω·m；

L——导体长度，单位为m；

S——导体截面积，单位为m²；

R——导体的电阻，单位为Ω。

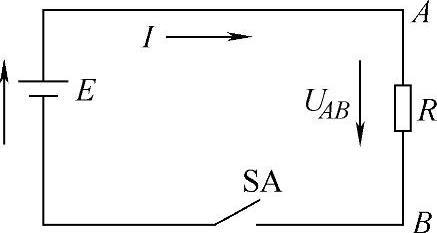
图3-28 电压及电动势的正方向

6）感抗容抗阻抗。当交流电通过电感线圈时，线圈会产生感应电动势阻止电流变化，有阻碍电流流过的作用，称感抗。它等于电感L与频率f乘积的2π倍。即：X_L=WL=2πfL。感抗在数值上就是电感线圈上电压和电流的有效数值之比。即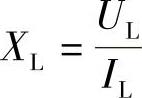：。感抗的单位是欧姆（Ω）。

当交流电通过电容时，与感抗类似，也有阻止交流电通过的作用，称容抗。它等于电容C乘以频率的2π倍的倒数。即：X_c=1/2πf_c=1/WC。容抗在数值上就是电容上电压和电流的有效值之比。即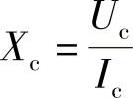：。容抗的单位是欧姆。

当交流电通过具有电阻（R）、电感（L）、电容（C）的电路时，所受到的阻碍称为阻抗（Z）。它的数值等于：Z²=R²+（X_L-X_c）²。阻抗在数值上就等于具有R、L、C元件的交流电路中，总电压U与通过该电路总电流I的有效值之比。即：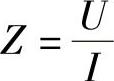

（2）欧姆定律

欧姆定律是表示电路中电流、电压、电阻三者关系的定律。

1）部分电路欧姆定律。不含电源的一段电路称为部分电路，如图3-29所示。在电阻R两端加上电压U时，电阻中就有电流I流过，三者之间关系为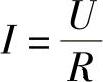

欧姆定律公式成立的条件是电压和电流的标定方向一致，否则公式中就应出现负号。

2）全电路欧姆定律。含有电源的闭合电路称为全电路，如图3-30所示。

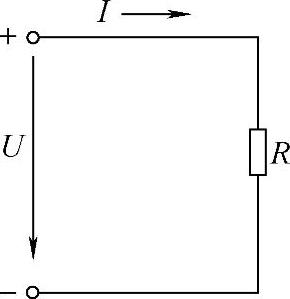
图3-29 部分电路

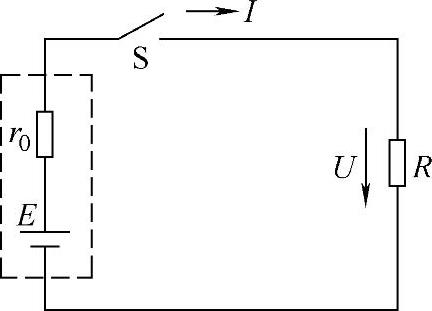
图3-30 全电路

图中虚线框内代表一个电源。电源除了具有电动势E外，一般都是有电阻的，这个电阻称为内电阻，用r₀表示。当开关S闭合时，负载R中有电流流过。电动势E、内电阻r₀、负载电阻R和电流I之间的关系用公式表示为

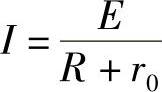
全电路欧姆定律还可以写为

E=IR+Ir₀=U+U₀

式中 U=IR——电源的端电压；

U₀=Ir₀——电源的内压降。

（3）电功和电功率

电流所做的功，叫电功；用符号W表示。电功的数学式为

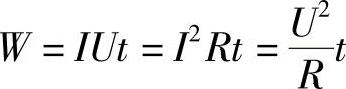
式中 U——导体两端的电压，单位为V；

I——电路电流，单位为A；

R——导体的电阻，单位为Ω；

t——通电时间，单位为s。

电功的大小与电路中的电流、电压及通电时间成正比，电功的单位为焦耳，另一个单位是千瓦·时（kWh）。它们之间的关系是1千瓦·时=3.6兆焦=3.6×10⁶焦耳（1kWh=3.6MJ=3.6×10⁶J）。(www.xing528.com)

单位时间内电流所做的功，叫做电功率。用符号P表示，即

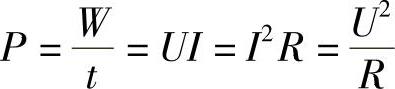
式中 U——导体两端的电压，单位为V；

I——电路电流，单位为A；

R——导体的电阻，单位为Ω；

t——做功的时间，单位为s；

W——电功，单位为J。

电功率的单位是瓦，功率较大时，电功率的单位是千瓦（kW）、兆瓦（MW）。（1MW=10³kW=10⁶W）。

当电流通过电阻时，要消耗能量而产生热量，这种现象称为电流的热效应。根据能量守恒定律，电路中消耗的功率将全部转换成热功率，即

P_R=0.24I²R

式中0.24为电、热功率的转换系数（热功当量），即每瓦电功率为0.24cal/s的热功率。

我们常用的电炉、白炽灯、电烙铁、电烘箱等都是利用电流的热效应而制成的电器。

（4）电源外部特性与电路的三种状态

1）电源的外部特性。在电动势不变的情况下，电源的端电压与电路中的电流大小及电源的内电阻大小有关。一般情况下，电流越大，电源的端电压就越低。

2）电源的三种状态。

①当电路接通，负载中有电流流过时，电路处于导通状态。

②若外电路与电阻值近似为零的导体接通时，电路处于短路状态。

③若电路中有断开处，电路中没有电流流过时，电路处于开路状态。电路处于开路状态时，电源的端电压与电动势相等。

（5）电阻的串、并联及混联

1）电阻的串联。凡是将电阻首尾依次相连，使电流只有一条通路的接法，叫做电阻的串联，如图3-31所示。电阻串联电路具有以下特点：

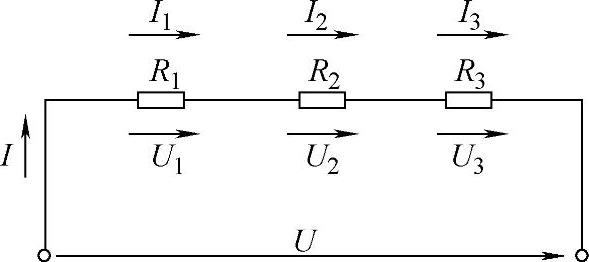
图3-31 串联电路

①串联电路中电流处处相等，即

I=I₁=I₂=I₃

②串联电路中总电阻等于各分电阻的和，即

R=R₁+R₂+R₃

③串联电路中总电压等于各分电压的和，即

U=U₁+U₂+U₃

④各电阻上的电压降之比等于其电阻比，即

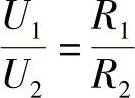
2）电阻的并联。将电阻两端分别连接在一起的方式，叫电阻的并联，如图3-32所示。电阻并联电路具有以下特点：

①并联电路中各电阻两端的电压等于电源电压，即

U=U₁=U₂=U₃

②并联电路中总电流等于各分电流的和，即

I=I₁+I₂+I₃

③并联电路等效电阻的倒数等于各并联支路电阻的倒数之和，即

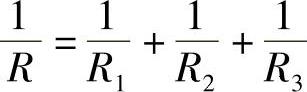
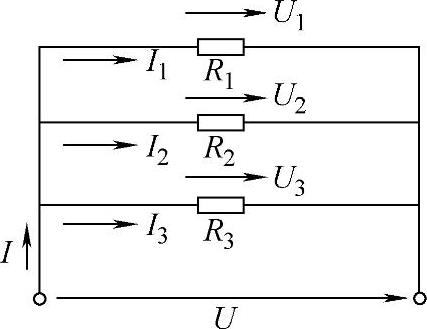
图3-32 并联电路

④各并联电阻中的电流及电阻所消耗的功率均与各电阻的阻值成反比，即

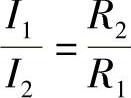
3）电阻的混联。电路中既有电阻的串联又有电阻的并联，则称混联电路。

（6）基尔霍夫定律

基尔霍夫定律包括第一定律和第二定律。它们是分析计算复杂电路不可缺少的基本定律。

1）基尔霍夫第一定律（节点电流定律）。对任一节点来说，流入（或流出）该节点电流的代数和等于零。其数学表达式为

∑I=0或∑I_进=∑I_出

电流正负的规定：一般取流入节点的电流为正，流出节点的电流为负。

2）基尔霍夫第二定律（回路电压定律）。在电路的任何闭合回路中，沿一定方向绕行一周，各段电压的代数和为零。

∑U=0或∑E=∑IR

在应用回路电压定律时，往往把电动势写在等式左边，把电压写在等式右边。

对于第二个表达式中各电动势和电压的正负确定方法如下：

①首先选定各支路电流的方向。

②任意选定沿回路的绕行方向（顺时针或逆时针）。

③若流过电阻的电流方向与绕行方向一致，则该电阻上的压降为正，反之取负。

④若电动势的方向与绕行方向一致，则该电动势取正，反之取负。