由于混凝土板的导热性能较差,当气温变化时,使板顶和板底产生温度差,其胀缩变形的大小也就不同,故引起板的翘曲。当板顶温度高于板底时,板的中部力图拱起,而在受约束后,板底将出现拉应力;反之,当板顶温度低于板底时,则板的四周会翘起,受到约束后板顶将承受拉应力。
分析表明,板的翘曲变形受到来自两方面的约束,如图9-10所示。一方面是板的截面在翘曲变形后仍保持为平面的倾向,它约束了由于温度沿板截面呈曲线分布而产生的那部分超出平面状态的应变;另一方面是板的自重、地基的反力和相邻板的钳制作用,使部分翘曲变形受阻。因薄板在温度梯度最大时的温度分布接近于直线,由第一方面约束所产生的内应力值较小,有时仅考虑第二方面约束。
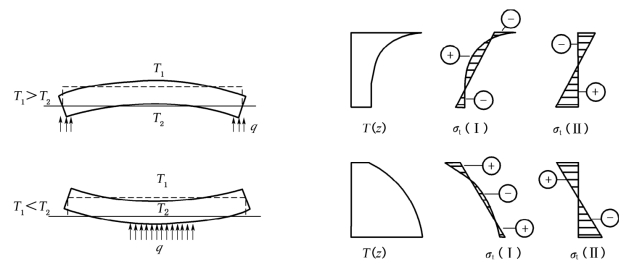
图9-10 板内不同温度分布时产生的应力分布
为了分析翘曲应力,Westergaard首先针对Winkler地基板,假设温度沿板厚呈直线变化,板和地基始终保持接触,板的自重忽略不计,从而导出了板仅受地基反力约束时在无限大板中部和窄而无限长板(或短而无限宽板)中部所产生的翘曲应力计算公式;R.D.Bradbury进而提出有限尺寸矩形板板中沿板长L和板宽B方向的翘曲应力计算公式如下:
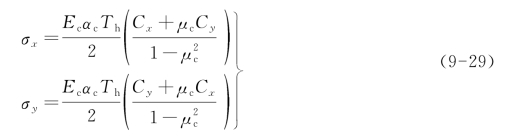
板边缘中点的翘曲应力为:
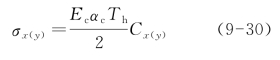
式中 Th——板顶与板底的温度差,℃;
Cx(y)——同L/l或B/l有关的翘曲应力系数,其数值可从图9-11中的曲线查取。
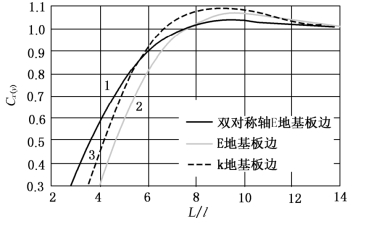
图9-11 弹性地基板温度翘曲应力系数Cx(Cy)和Dx(Dy)值图
图9-11中标注的“双对称轴E地基板边”是指路面横向分布有两块板及以上的情形,考虑到横向板块间以纵缝作为对称轴、纵向板块间以横缝作为对称轴发生翘曲,因此,弹性地基的水平约束亦是以纵缝和横缝作为对称轴的,即弹性地基的基础在水平向是与路面板同尺寸的,而不是一般E地基板基础在水平向是无限大的情况,这样的地基板称为双对称轴E地基板。
由图9-11可知,板的翘曲应力随板长的增加而加大,但板长到一定程度后,应力值差别就不大了;而板的相对刚度半径对翘曲应力的影响则相反。
半无限地基板的温度翘曲应力,目前尚无解析解。同样,可以用有限元法,采取Westergaard计算翘曲应力的假设,对不同参数情况进行大量的计算,并按式(9-29)和式(9-30)的形式加以整理,而得到图9-11中的曲线1和曲线2,供分别查取板边中点的翘曲应力系数使用。
当混凝土板较厚时,混凝土路面板内的温度沿截面的非线性分布将比较显著,采用温度沿截面呈线性分布的假设,按板顶与板底温度差确定的温度梯度来计算翘曲应力会得到较大的偏差(图9-10)。为此,温度翘曲应力的计算中应考虑由于温度非线性分布而板截面保持平面变形所产生的内应力的影响。计入此温度内应力的翘曲应力表达式为:板中部:
 (https://www.xing528.com)
(https://www.xing528.com)
板边缘中点:

式中,Dx为x轴(板长)方向考虑温度沿板厚非线性分布的温度(翘曲)应力系数:
![]()
计算板中部翘曲应力时,Cx以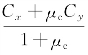 代替。
代替。
上述各式中,将下标x与y互换,即可得到y(宽度)方向的温度应力。计算板边缘中点的翘曲应力时,翘曲应力系数Cx(y)绘制成图9-11所示的曲线,以便查用。
【例9-4】公路自然区划Ⅱ区拟新建一条二级公路,路面宽7 m,板长5 m,板宽3.5 m,板厚0.24 m,混凝土模量Ec=30 000 MPa,泊松比μc=0.15,热膨胀系数αc=0.000 01/℃,板下地基综合回弹模量Es=100 MPa,地基泊松比取为μs=0.25,求路面板边缘中点的最大温度应力。
【解】查公路自然区划表,最大温度梯度Tg=88℃/m,Th=hTg=0.24 m×88℃/m=21.12℃,由式(9-17)求得水泥混凝土路面板的相对刚度半径l。
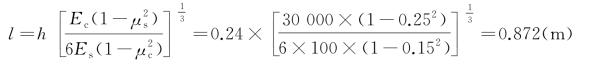
板长与相对刚度半径之比:![]()
查图9-11中的曲线1,得到翘曲应力系数Cx=0.860。
由式(9-33)计算Dx。
Dx=1.77×0.86×e-4.48×0.24-0.131×(1-0.86)=0.501
由式(9-32)计算路面板边缘中点的最大温度应力σtmax为:
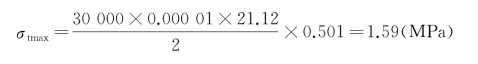
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




