铺面工程学第2版：半无限地基板的解法

1.解析解

半无限地基上无限大板受到集中或圆形均布荷载作用时，属于轴对称课题，可通过求解板的挠度方程，进而得到弯矩关系式。

距荷载作用中心（坐标原点）r处的挠度为

式中　l——半无限地基板的相对刚度半径，即

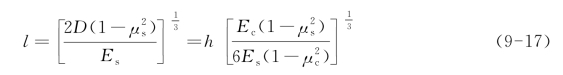
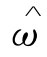——挠度系数，随r/l和a/l而变，如图9-6所示。

图9-6表明，荷载圆半径a对挠度系数的影响不大。因而，对于圆形均布荷载，可以按集中荷载计算其挠度值。距集中荷载作用点r处板在单位宽度的径向弯矩和切向弯矩为

式中，Mr，Mt分别为径向和切向弯矩系数，其值随r/l而变，可由表9-1查得。

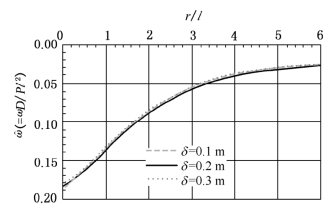
图9-6　半无限地基上板的挠度系数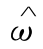（μc=0.15）

图9-7　距离集中荷载作用点为r处的弯矩

圆形均布荷载作用下板内产生的最大弯矩（位于荷载中心处，在各个方向均相同）为

式中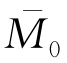，为荷载中心下（r=0）板的弯矩系数，其值随δ/l而变，可查表9-1；但当δ＜1.724h时，应按式（9-9）以当量计算半径b代替。

必须指出，只有当荷载作用中心与板最短边缘的距离大于相对刚度半径的1.5倍时，才能应用上述无限大板的公式解算弯矩Mr，Mt和M0，再按式（9-20）计算板的应力：

对比两种地基上无限大板的解可知，如果二者相对刚度半径相等，则所得板的应力是一致的。因此，采用式［9-8（a）］，亦能计算半无限地基板的板中应力。

表9-1　弯矩系数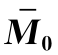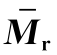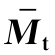，，值（μc=0.15）

续表

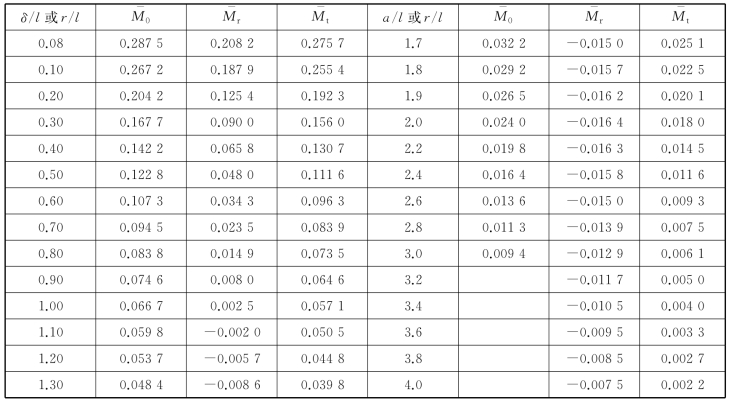
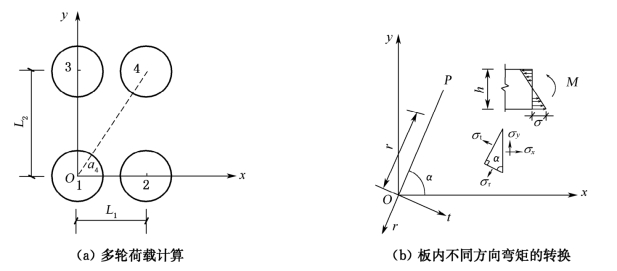
图9-8　多轮荷载时的弯矩计算

当板中受到多个车轮荷载作用时，如图9-8所示，可取其中一个车轮作为主轮，按均布荷载考虑，其他各轮按集中荷载考虑，叠加它们的影响。叠加时需注意应力的方向。如在计算点统一取正交的x，y方向，则各轮在该点的径向弯矩Mr和切向弯矩Mt，均应转换为x，y方向的弯矩Mx和My，再分别叠加起来。根据材料力学中所述单元体斜截面上的应力关系，可推得板内不同方向弯矩的转换公式：

式中，α为集中荷载作用点与弯矩计算点连线同x轴的夹角。

【例9-1】JN360型双后轴车，双后轴一侧共四个车轮（图9-8），轮间距离L1=34 cm，L2=135 cm，每个车轮的荷载P=27.5 kN，轮压p=0.7 MPa。混凝土路面板厚h=22 cm，弹性参数Ec=30 000 MPa，μc=0.15；地基参数Es=180 MPa，μs=0.30。试分析板中最大应力值。(www.xing528.com)

【解】如图9-8所示，取1号车轮作为主轮，计算该荷载中心下的应力。

由式（9-17），可求得板的相对刚度半径：

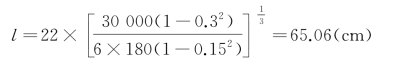
1号轮载作用圆的半径a，按下式计算：

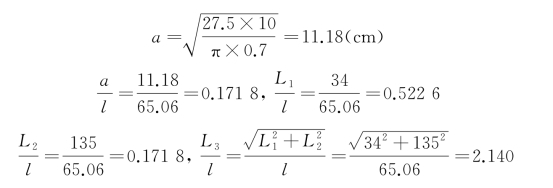
由表9-1查得各轮载的弯矩系数，按表9-2计算四个车轮荷载在1号车轮下产生的弯矩系数。

表9-2　多轮荷载的弯矩系数计算

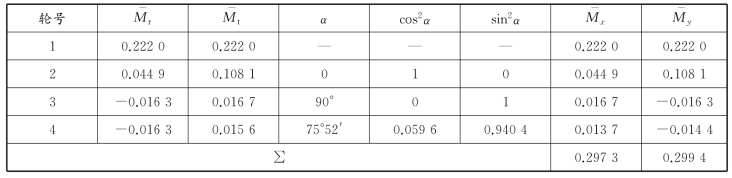
板中承受的弯拉应力：

由此可见，多轴多轮荷载所产生的板中应力，并不比其中单轴双轮组的应力大多少，有时甚至更小些，这取决于其他轮轴荷载的应力方向，相对于主要应力方向来说，是切向还是辐向，同时还取决于轮（轴）距与相对刚度半径的比值。

半无限地基板边角荷位的应力分析，目前尚无解析解，只有采用近似的数值计算方法，如有限元法等。

2.有限元解

有限元技术的发展和应用给路面结构分析带来了革命性的进展，张（Cheung）和森克维奇（Zienkiewicz）于1965年推导了分析液体和固体两种弹性地基上板的有限元法。1970年代起，S.K.Wang，黄仰贤，Eberhardt和S.T.Wang等人先后将有限元法应用于水泥混凝土路面，分析了Winkler地基、弹性半空间地基、层状地基上混凝土路面的挠度和应力，探讨了接缝传荷和地基部分脱空等情况的计算方法。我国从20世纪70年代后期起，同济大学姚祖康等开始将有限元法用于混凝土路面的计算分析，奠定了我国水泥路面分析的基础。

国际上水泥路面有限元分析软件主要有KENSLAB，ILLI-SLAB，J-SLAB，ISLAB2000和Ever FE等。

大量计算结果表明，在单轴荷载情况下，轴载作用于板纵缝边缘中部时（即两侧双轮中有一侧靠贴纵边，另一侧在板内，图9-9（a）应力最大；仅双轮组轮载作用于板横向边缘中部时的应力大于轴载作用于板横边时的应力［图9-9（b）］；双轮组轮载作用于板中时应力最小，也小于轴载作用于板中部时的应力［图9-9（c）］。

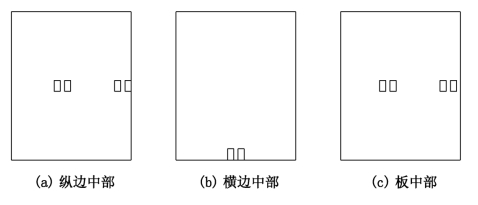
图9-9　有限元法的计算荷位

而当采用刚性、半刚性基层时，基层最大荷载应力位置随基层超宽（纵向、横向）不同，分别落在板角隅下方基层底面和纵边边缘中部下方基层底面，分别对应角隅荷位和纵缝边缘中部荷位。通过回归分析，得到单层板和等尺寸双层板纵缝边缘中部荷位下水泥混凝土路面结构各层的荷载应力计算式。

纵缝边缘中部荷位下等尺寸双层板面层、基层荷载应力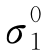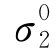，（MPa）公式如下：

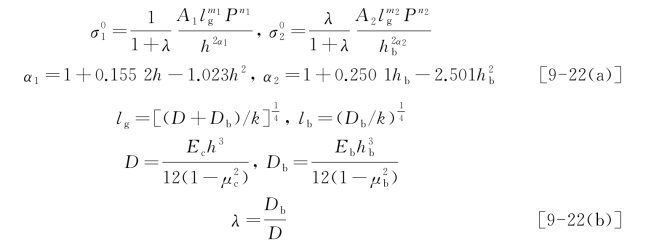
式中　P——单轴、双轴或三轴总轴重，kN；

h，hb——分别为混凝土面层和基层厚度，cm；

lg，lb——分别为双层板总的相对刚度半径和基层相对刚度半径，m，按式［9-22（b）］求算；

A，m，n——回归系数，见表9-3。

上述回归公式适用于板的相对刚度半径lg=50～140（cm）的范围内，其相对误差一般不超过±5%；否则，误差会大些。

试验研究发现，荷载作用于板角时，Winkler地基板的有限元解要比半无限地基板的解更符合实际。

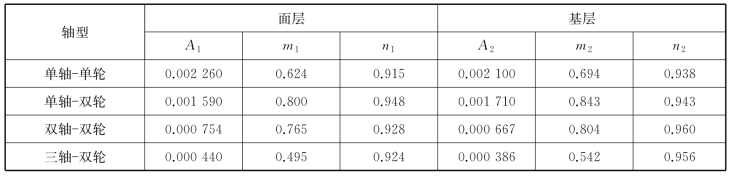
表9-3　回归系数A，m，n值