Winkler地基板解析解及Westergaard方法

Westergaard采用Winkler地基假设，分析了图9-3所示的三种典型轮载位置下的挠度和弯矩，得到最大弯拉应力、位移的计算公式：

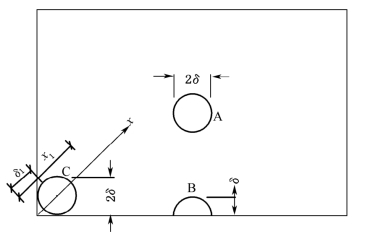
图9-3　无限大板三种典型轮载荷位

（1）轮载作用于无限大板的中央，压力均布于半径为δ的圆面积内；

（2）轮载作用于一个半无限大板直线边的边缘，压力均布于半径为δ的半圆内；

（3）轮载作用于一个大板的两个直角边的角隅处，压力均布于半径为δ的圆面积内，圆心距角隅点的距离为。

1.轮载作用于板的中央（板中荷位A）

当作用的荷载为集中荷载P时，Winkler地基上无限大板顶面的挠度和底面的弯拉应力可由式（9-6）计算：

式中　l——路面板和地基的相对刚度半径：

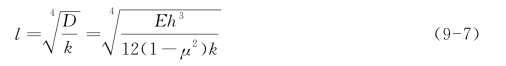
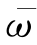（ξ）——挠度系数，其值随ξ（=r/l）而变，如图9-4（a）所示；

r——距荷载作用点的距离；

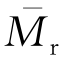（ξ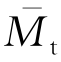），（ξ）——分别为径向和切向弯矩系数，其值随ξ而变，如图9-4（b）所示。

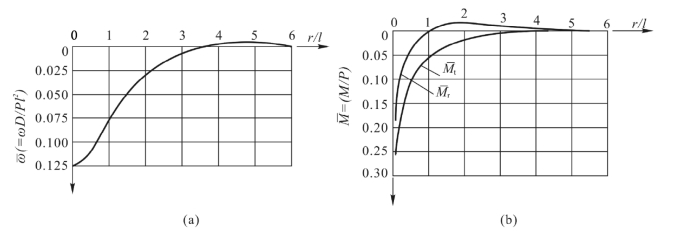
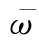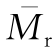图9-4　集中荷载作用于板中时（ξ），（ξ）和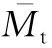（ξ）系数曲线（μ=0.15）

由图9-4可以看出，当r=0时，弯矩为无限大；随着r的增大，挠度和弯矩迅速减小，特别是径向弯矩，衰减得更快；在r=l附近即转为负值，并在r=2l附近负弯矩达到最大值；在r=4l附近和均转为负值。

将车轮荷载P处理成圆形均布竖直荷载（其车辆荷载当量圆半径为δ，压强为p），H.M.Westergaard［1，2］给出了圆形荷载作用于板中的应力、挠度公式：

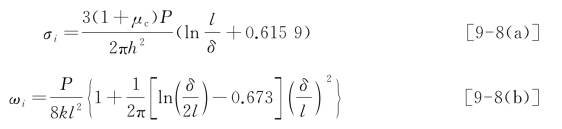
式中　σi——板中应力；

ωi——板中挠度。

当轮载作用面积较小时，压强p可能很大。这时，如果仍采用薄板理论计算应力，会得出偏大的结果。通过分析薄板与厚板计算理论计算结果的差异，用式（9-9）中的b替代式（9-8）中的δ，计算应力和挠度。

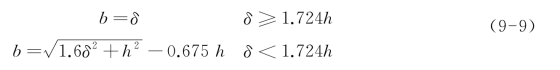
对于水泥混凝土路面，同济大学的研究发现其弯沉盆曲线上具有比沥青路面更为明显的惰性点现象，这非常有助于路面结构的进一步分析［8］。

2.轮载作用于板边中部（板边荷位B）

H.M.Westergaard于1926年、1933年和1948年分别研究了板边荷载作用下的应力和挠度，并在1948年的论文中提出了板边作用椭圆形和半椭圆形荷载产生的最大应力和挠度的一般解，将椭圆最大和最小半轴长度转换成接触圆半径δ，可得到相应的圆形或半圆形荷载的解。下面列出圆形荷载作用下的应力、挠度计算式。

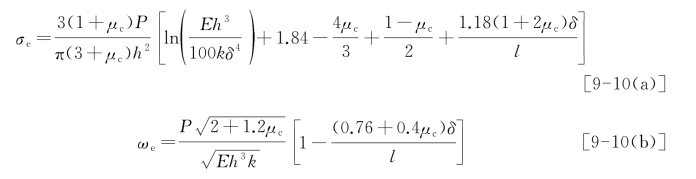(www.xing528.com)

美国阿灵顿（Arlington）试验路试验表明，若板边与地基脱开，实测应力值将比式（9-10）的计算值偏高10%左右。

3.轮载作用于板的角隅（板角荷位C）

Westergaard于1926年采用最大位能原理给出了圆形荷载作用于板角的应力、挠度计算的近似式。

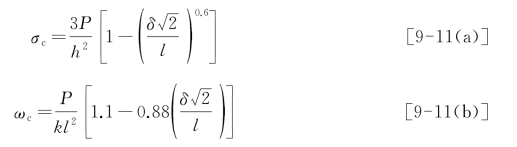
式中　ωc——板角挠度；

δ——接触面积半径；

P——车轮荷载；

l——路面板和地基的相对刚度半径；

h——路面板厚度；

k——地基反应模量。

Westergaard发现，板的最大应力出现在半角顶面沿分角线距角隅处。

A.M.Ioannides等［9］应用有限元法评估Westergaard板角受荷的解，他们建议采用式（9-12）计算板角的应力和挠度：

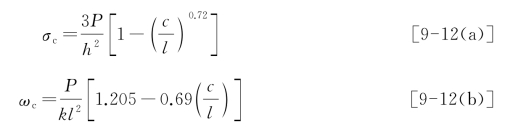
式中，c为方形接触面积的边长。

最大应力出现在距角隅1.80c 0.32l 0.59处，若荷载作用在圆形面积上，c值由式（9-13）确定

在温度梯度和地基塑性变形的影响下，板角也会同地基脱开。试验表明，板角上翘时，实测应力值要比按式［9-12（a）］的计算结果大30%～50%。对此，E.F.Kelley［3］提出了经验修正公式：

总结上述三种受荷情况下的最大应力计算公式，可以统一写为

式中，C为应力系数，可由图9-5查得。

由图9-5可见，在同一轮载和路面结构条件下，板中受荷时产生的最大应力值低于板边和板角受荷时的最大应力值，约为未脱空的板边最大应力的2/3左右。板角受荷时产生的最大应力，在板角未翘起的情况下低于板边受荷时的最大应力；但在板角翘起时，则超过板边受荷的最大应力。

Westergaard公式基于板与土基完全接触的假设，没有考虑板底脱空对应力挠度的影响。由于实际问题的复杂性，诸如板底脱空、复杂边界条件、接缝传力杆传荷、多荷载构形及位置变化，以及基层、地基等力学非线性性状等众多因素的影响，上述理论解法难以给出相应的解算结果。

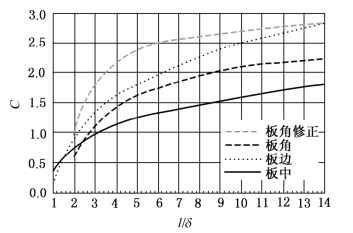
图9-5　应力系数C值图（μc=0.15）