水泥混凝土路面面层的刚度很大，具有很好的板体性和荷载扩散能力，通常设置接缝将面层划分为在平面上有限尺寸的板块，平面上的尺度（一般4～6 m）远大于厚度方向上的尺度（一般10～50 cm）。在车辆荷载作用下，水泥混凝土路面上产生的挠度很小（一般小于1 mm），比厚度小两个数量级。鉴于水泥混凝土路面的这些特性，通常将其简化为弹性地基上的小挠度薄板模型进行结构分析。
混凝土面层板为具有弹性常数Ec（弹性模量）和μc（泊桑比）的等厚度弹性体，面层板以下的基（垫）层和路基，可以看作弹性地基，它对面层板仅有竖向的支承反力，地基与混凝土板之间为光滑接触，没有摩擦力；地基和板始终保持着竖向变形的连续性（完全接触），即使地基反力为负向（向下）时也是如此。此外，还需要做出如下三项重要的基本假设：
（1）同其他应力分量和应变分量相比，垂直于中面方向的正应力σz和正应变εz很小，可以忽略不计。由此，竖向位移（即挠度）ω沿板厚各点具有相同的数值，仅是平面坐标（x，y）的函数。
（2）弯曲前垂直于板中平面的直线纤维，在弯曲后仍保持为直线并垂直于中曲面，因而，横向剪切应变γxz=γyz=0。
（3）中面上各点无平行于中面（x和y方向）的位移。
这三项假设将一个处于三维应力状态的路面结构简化为一小挠度薄板问题，如图9-1所示。依据上述假设，可由几何方程和物理方程推导出薄板的挠曲面微分方程（挠度与荷载的关系式）：
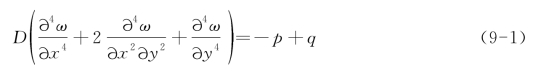
采用圆柱坐标时，则上述挠曲面方程可改写为
式中 p——板顶作用的荷载；
q——板底地基反力。
D——板的弯曲刚度，其表达式为
式中 h——板的厚度；
Ec，μc——混凝土板的模量和泊松比。
图9-1 板的微分单元受力分析
在上述微分方程中，地基反力q随地基的特性和板的挠度W而异。为了建立地基反力同挠度之间的关系，通常采用两种不同的地基假设，即Winkler地基假设和弹性半空间地基假设。(www.xing528.com)
1.Winkler地基
早在1876年，E.Winkler将地基视为水平向互不联系的弹簧，提出了地基的弹簧模型，通常称为Winkler地基假设。1884年，H.Hertz为了解决冰块的承载力问题，将冰块视为支承于稠密液体基础上（Winkler地基）的薄板，采用弹性理论，求得了静荷作用时冰块的极限承载力，这算是弹性地基薄板理论的最早工作。
1926—1948年间，H.M.Westergaard对混凝土路面的应力、挠度做了广泛的研究，根据稠密液体地基上无限大板或半无限大板假设，推导了三种荷载位置和温度翘曲应力的计算公式。1939年，Kelley根据Arlington试验路结果对Westergaard的板角、板边公式做了修正，提出了丧失部分地基支承情况下板角、板边应力的经验公式［3］。
Winkler地基板模型如图9-2（a）所示，即将刚度大的水泥混凝土面层看作支承于Winkler地基上的小挠度弹性板，或将刚度较大的水泥混凝土板和板体性较大的基层看作支承于Winkler地基上的双层小挠度弹性板，如图9-2（b）所示。
假设地基上任一点的反力仅同该点的挠度成正比，而同其他点无关，即
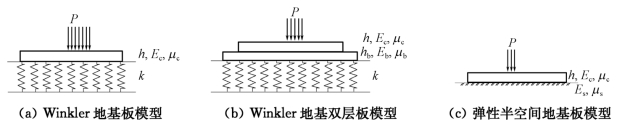
图9-2 地基薄板模型
式中 k——地基反应模量。
2.弹性半无限地基
将路面板下地基视为弹性半空间体，A.H.A.Hogg和O.Я.Щехтер等［4，5］求得无限大板在轴对称荷载作用下的应力和位移解答，此即为弹性半无限地基薄板理论，这一理论被一些国家的公路部门采用。迄今尚无圆形均布荷载作用于弹性半无限地基大板板角和板边时的荷载应力和挠度解析解，荷载作用于大板板中时，Losberg［6］给出了荷载应力计算公式。
假设地基为弹性半无限体，如图9-2（c）所示，其性质用弹性模量Es和泊松比μs来表征。若地基表面上作用轴对称荷载［反力q（r）］，则地基表面任一点的挠度ω（r）为
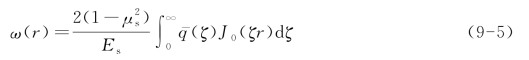
式中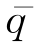 
（ζ）——反力q（r）的零阶Hankel变换式；
J0（ζr）——零阶Hankel函数。
除上述两种常用的地基模型外，苏联的Pasternak［7］提出了一种双参数地基模型，除Winkler地基反应模量参数外，再引入一项考虑弹簧间水平联系的参数——剪切模量G，通过剪切模量G来调节地基在水平方向传递荷载的能力，则这种地基薄板理论被称为Pasternak地基板理论。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
